Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

При попадании точки в области диаграммы, для которых не определён закон распределения, выдвижение гипотетического закона должно осуществляться на основании каких-либо дополнительных априорных соображений.

П р и м е р 7.2. В условиях примера 7.1 выбрать нулевую гипотезу аналитическим способом.

▼ По формулам (7.1.5) вычисляем оценки центральных моментов третьего и четвёртого порядков:

;

                                       .                   

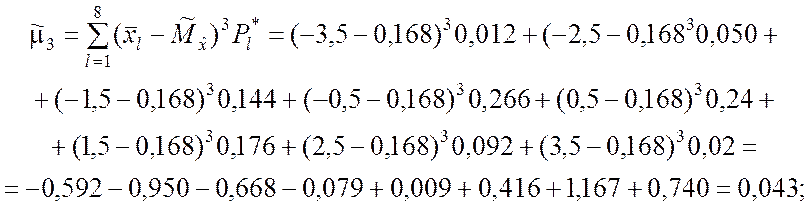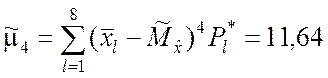По формулам (7.1.4) вычисляем оценки коэффициента асимметрии и коэффициента эксцесса:

                                        ;

                                  .              

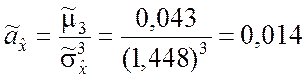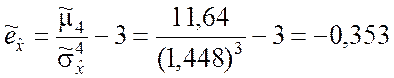Точку (; ) = (0,0001;–0,353) наносим на диаграмму, рис.7.2. Данная точка находится в непосредственной близости от точки (0; 0). Следовательно, принимается нулевая гипотеза о нормальном распределении отклонений по вертикали при стрельбе в мишень.

▲

Проверка гипотезы о виде закона распределения выполняется после решения предыдущей задачи, т.е. выбора теоретического распределения.

7.1.3. Проверка гипотез о законах распределения по методу К.Пирсона

Задача проверки гипотезы о виде закона распределения формулируется следующим образом.

Пусть в результате эксперимента получена случайная выборка , ,…, и для неё выбран теоретический закон распределения, характеризуемый функцией распределения  или плотностью распределения .

Необходимо на основании обработки и анализа полученной выборки проверить гипотезу H₀ о том, что исследуемая случайная величина подчинена выбранному закону распределения.

В настоящее время существует ряд методов решения данной задачи, однако наибольшее распространение получил метод К. Пирсона. Достаточно употребляемыми являются также методы А.Н. Колмогорова и Н.В. Смирнова  [4, 6, 12]. Указанные методы отличаются друг от друга видом меры рассогласования между статистическим и гипотетическим законами распределения. Так, в методах А.Н. Колмогорова и Н.В. Смирнова такой мерой является функция разности между статистической функцией распределения  и функцией распределения  гипотетического закона:

                                            .

В методе К. Пирсона в качестве таковой используется функция разности между частотой и вероятностью попадания случайной величины в заданные интервалы:

                                                  ,                    (7.1.6)

где j – номер интервала.

Рассмотрим метод К. Пирсона более подробно. Мера расхождения (7.1.6) в явном виде представляется суммой квадратов разностей между частотой и вероятностью попадания случайной величины  в интервалы, на которые разбивается множество возможных значений этой величины:

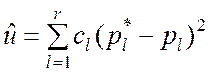                                               ,                  (7.1.7)

где r – число интервалов; l – номер интервала.

Коэффициенты c_l введены в выражение (7.1.7) для учёта того, что абсолютные значения разностей  неравнозначны при различных значениях p_l. Действительно, одно и то же значение разности  является малозначимым при большой величине p_l и представляет собой заметную величину, если вероятность p_l мала.

К. Пирсон показал, что коэффициенты c_l целесообразно брать обратно пропорциональными вероятностям p_l. При этом, если данные коэффициенты определять на основе выражения

                                                 ,   ,                             

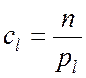то при больших значениях n закон распределения случайной величины

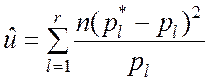                                                                  (7.1.8)

не зависит от вида распределения случайной величины  и объёма выборки n, а зависит только от числа интервалов r. Кроме этого при увеличении n закон распределения случайной величины (7.1.8) приближается к распределению хи-квадрат  [6].

Докажем это утверждение.

Рассмотрим случайную величину  – число попаданий случайной величины  в l-й интервал. Эта случайная величина распределена по биномиальному закону с характеристиками

                                    ,    .                

Однако при достаточно большом n величину  на основании теоремы Муавра-Лапласа можно считать распределённой по нормальному закону с теми же характеристиками. Выполняя нормирование случайной величины , получим