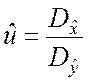Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 8

                                                        .                           (7.2.9)

Учитывая оценки (7.2.8) при условии, что нулевая гипотеза справедлива, на основе отношения (7.2.9) получаем следующее выражение показателя согласованности:

                                         .                     

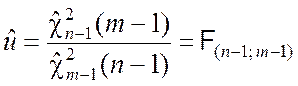Таким образом, показатель согласованности представляет собой случайную величину, подчинённую закону распределения Фишера со степенями свободы  f₁ = n – 1  и  f₂ = m – 1. Как известно, распределение Фишера зависит только от значений степеней свободы и уровня значимости, а от других параметров не зависит.

Критическая область в зависимости от вида конкурирующей гипотезы строится по-разному. Как и ранее, рассмотрим три вида конкурирующей гипотезы:

                                   ¹ ;     > ;     < .

Построение критических областей для каждого из этих видов осуществляется следующим образом.

1. H₀: = ;    H₁: ¹ .

В этом случае строят двустороннюю критическую область, исходя из того, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна уровню значимости a. При этом достигается наибольшая мощность критерия проверки, когда вероятности попадания показателя согласованности в каждый из двух интервалов критической области будут одинаковы и равны a/2. Таким образом, при построении критической области должны выполняться следующие условия (рис.7.4):

                                              

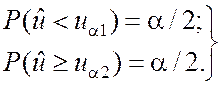
Правая критическая точка u_a2 может быть найдена непосредственно по таблице критических точек распределения Фишера (приложение 5). При этом входами в таблицу будут величины  a/2,   f₁ = n – 1,   f₂ = m – 1.  В результате имеем

                                            .

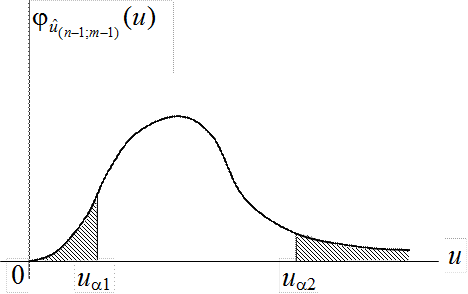
Рис.7.4. Двусторонняя критическая область

Однако левых критических точек данная таблица не содержит и найти непосредственно u_a1 невозможно. В связи с этим для нахождения левой критической границы u_a1 необходимо использовать следующий приём.

Рассмотрим события

                                  F_{(n–1; m–1)} < F_a1    и   .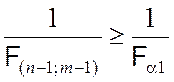

Так как эти события эквивалентны, то их вероятности равны:

                           .

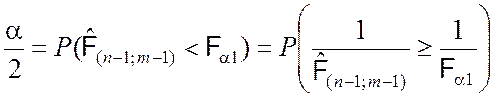Как известно [1], случайная величина  также подчиняется закону распределению Фишера со степенями свободы  f₁ = m –1, f₂ = n – 1. Поэтому значение 1/F_a1 может быть найдено как верхний 100(a/2)-процентный предел этого закона распределения:

                                                 .

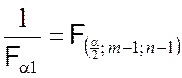Таким образом, для определения 1/F_a1 необходимо войти в таблицу критических точек распределения Фишера с аргументами   a/2,  f₁ = m –1, f₂ = n – 1. Значение левой критической границы определяется как величина, обратная значению, найденному по таблице.

Учитывая изложенное выше, правило проверки гипотезы о равенстве дисперсий можно сформулировать в следующем виде.

а). Назначается уровень значимости a и по таблице критических точек распределения Фишера находятся критические границы u_a1 и u_a2. При нахождении критической границы u_a2 в таблицу следует входить с аргументами   a/2,   f₁ = n – 1,   f₂ = m – 1,  а при определении критической границы u_a1 – с аргументами   a/2,   f₁ = m – 1,   f₂ = n –1. В последнем случае табличное значение   используется для определения критической границы u_a1 из выражения

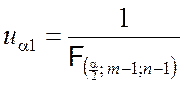                                                 .                  (7.2.10)

б). Вычисляется значение показателя согласованности

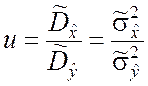                                                    .                    (7.2.11)

в). Проверяется неравенство

                                                    u_a1 < u < u_a2.

Если оно выполняется, то наблюдаемое значение показателя согласованности попадает в область допустимых значений. В этом случае делается вывод об отсутствии существенного различия между сравниваемыми дисперсиями и гипотеза H₀ принимается. Если u < u_a1 или u > u_a2, то нулевая гипотеза отвергается.