Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 2

▼ Нормальный закон распределения

                                           

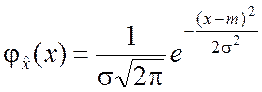
зависит от двух параметров:  и . Подберём эти параметры так, чтобы сохранить первые два момента – математическое ожидание и дисперсию статистического распределения. Оценку математического ожидания вычисляем по формуле (5.1.4):

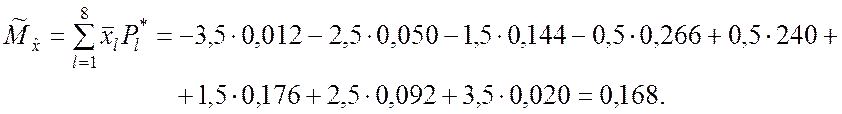
Оценку дисперсии вычисляем по второй формуле (5.2.14). Для этого находим оценку второго начального момента

                                             .

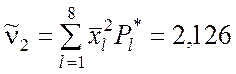В итоге получаем

                            .

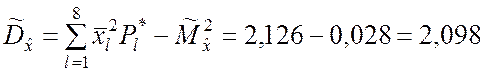В соответствии с методом моментов должны выполняться условия

                                                 .

Это означает, что

                                       .

Выражение нормального закона распределения принимает вид

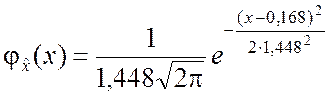                                       .         (7.1.3)

Вычисляем значения функции (7.1.3) на границах разрядов, результаты сводим в табл.7.2.

Таблица 7.2

Значения плотности распределения нормального закона (к примеру 7.1)

x	–4	–3	–2	–1	0	1	2	3	4
	0,004	0,025	0,090	0,199	0,274	0,234	0,124	0,041	0,008

На одном графике (рис.7.1) строим гистограмму и выравнивающую её кривую распределения.

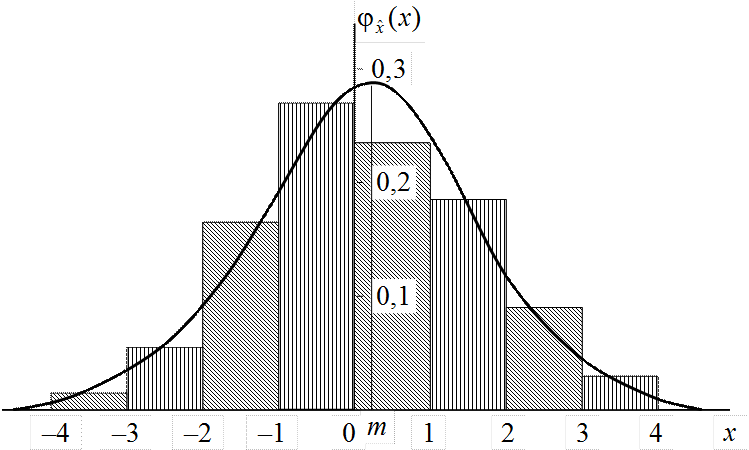
Рис.7.1. Гистограмма и теоретическая кривая распределения (к примеру 7.1)

Из графика видно, что теоретическая кривая распределения  сохраняет в основном существенные особенности статистического распределения. Но при этом она свободна от случайных неправильностей хода гистограммы, которые, по-видимому, могут быть отнесены за счёт случайных причин. Для более серьёзного обоснования последнего суждения необходимо выполнить проверку гипотезы о принятом законе распределения.                                                                                                 ▲

Выравнивание статистического ряда теоретической кривой распределения может рассматриваться как выдвижение нулевой гипотезы о виде распределения. Но эта задача может быть решена и аналитически.

7.1.2. Выбор нулевой гипотезы аналитическим способом

Для аналитического выбора нулевой гипотезы может быть использована следующая методика. По данным эксперимента определяются статистические оценки коэффициента асимметрии  и коэффициента эксцесса :

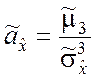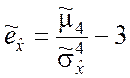                                           ;     ,              (7.1.4)

где                       ;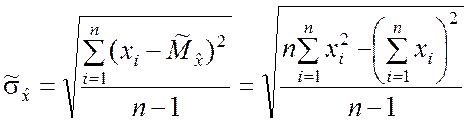

                            ;       .

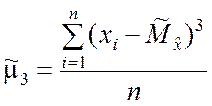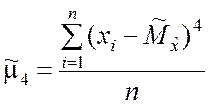При большом объёме выборки оценки центральных моментов третьего и четвёртого порядков могут вычисляться по формулам, аналогичным (5.2.11) для дисперсии:

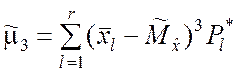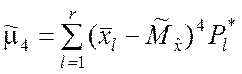;     .                                                         (7.1.5)

В теории распределений [12] доказано, что каждому закону свойственно определённое соотношение между коэффициентами асимметрии и эксцесса, т.е. может быть построена диаграмма, изображённая на рис.7.2.

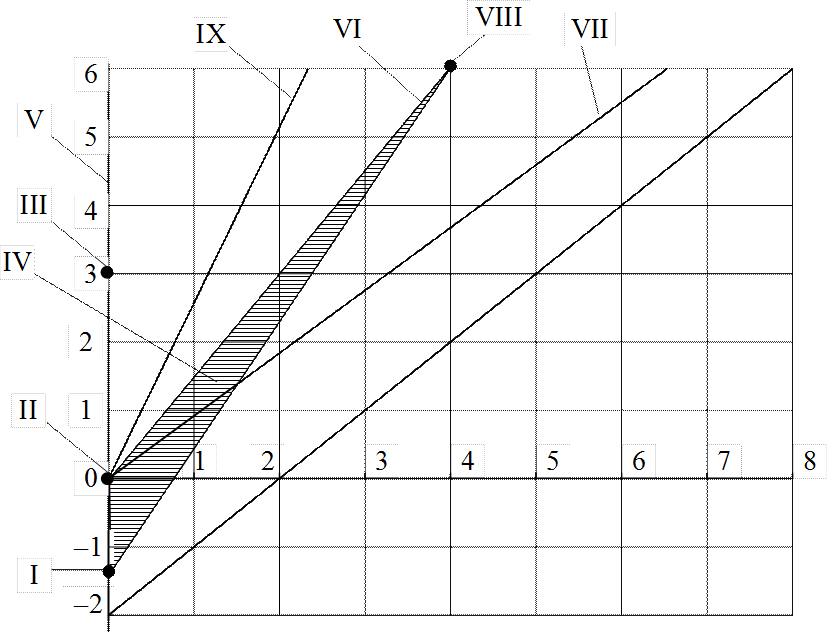
Рис.7.2. Диаграмма соотношений между коэффициентами асимметрии и эксцесса

На представленной диаграмме выделены следующие характерные точки, прямые и области. Точки (0; –1,2), (0; 0), (0; 3), (4; 6) отвечают соответственно равномерному и нормальному распределениям, распределению Лапласа и показательному распределению. Так, для любого нормального закона  = 0,  = 0, что и определяет координаты точки (0; 0). Гамма-распределение, логарифмически нормальное распределение, распределение Стьюдента и Пуассона показаны на диаграмме прямыми, а бета-распределение представлено областью. При этом обозначения следующие: I – равномерный закон, II – нормальный закон; III – закон Лапласа; IV – бета-распределение; V – закон Стьюдента (прямая, совпадающая с осью ординат); VI – гамма-распределение; VII – закон Пуассона; VIII – показательный закон; IX – логарифмически нормальное распределение.

Знание оценок коэффициентов асимметрии и эксцесса позволяет приближённо определить гипотетический закон распределения. Для этого по полученным значениям оценок на диаграмму наносится точка (;). Если она окажется вблизи точки, прямой или области, соответствующих одному из распределений, то последнее и следует выдвинуть в качестве гипотезы.