Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 7

2. H₀:  = ;     H₁:  > .

Такой случай возможен, если априорные сведения позволяют предположить, что  > . В этом случае строят такую правостороннюю критическую область, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна a:

                                                   .                     (7.2.6)

Для того чтобы критическую точку найти с помощью функции Лапласа, перепишем выражение (7.2.6) в виде

                           .        

Из предыдущего выражения получим

                                                  

и, следовательно,

                                                            (7.2.7)

Правило проверки гипотезы для рассматриваемого случая.

а). Назначается уровень значимости a и в соответствии с (7.2.7) по таблице приложения 4 определяется величина u_a. При этом в таблицу следует входить  со  значением 1–2α,

б). Определяется величина u  по формуле (7.2.5).

в). Проверяется условие u > u_a. Если оно выполняется, гипотеза H₀ отвергается, в противном случае принимается.

3. H₀:  = ;     H₁:  < .

При указанной формулировке конкурирующей гипотезы левостороннюю критическую область строят так, чтобы вероятность попадания в неё показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости:  .      

Учитывая, что показатель  имеет симметричное распределение относительно нуля, заключаем, что точка u_a1 симметрична такой точке u_a > 0, для которой , это значит u_a1 = –u_a. Следовательно, методика определения u_a1 полностью совпадает с методикой предыдущего случая, только полученное значение берётся с отрицательным знаком.

Правило проверки гипотезы также аналогично рассмотренному выше правилу, за исключением последнего пункта, а именно, если u < u_a1, нулевая гипотеза отвергается, в противном случае – принимается.

Выше предполагалось, что случайные величины  и  распределены нормально, а их дисперсии известны. При этих предположениях показатель согласованности гипотезы распределён по нормальному закону с параметрами  = 0,  = 1. Если хотя бы одно из предположений не выполняется, описанный метод проверки гипотезы о равенстве математических ожиданий неприменим. Однако при больших объёмах независимых выборок (³ 30 вариантов каждая) оценки математических ожиданий и дисперсий распределены приближённо нормально и закон распределения  можно считать близким к нормальному. В этом случае проверку гипотезы можно проводить по описанной выше методике, подставляя в формулу (7.2.5) оценки дисперсий, но к полученным результатам следует относиться с осторожностью.

7.2.2. Проверка гипотез о равенстве дисперсий

Проверка гипотез о равенстве дисперсий – одна из важнейших задач статистической обработки экспериментальных данных. На практике задача сравнения дисперсий возникает, если требуется сравнить погрешности показаний приборов, точность методов измерений и т.д.

Сформулируем задачу проверки гипотезы о равенстве дисперсий. Пусть имеются две случайные величины  и , каждая из которых подчиняется нормальному закону распределения с дисперсиями  и . По независимым выборкам  x₁, x₂,…,x_n  и  y₁, y₂,…,y_m  найдены оценки дисперсий:

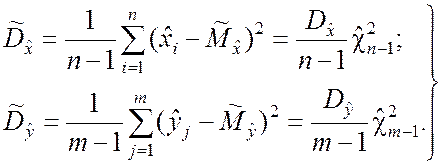                               , (7.2.8)

где ,  - хи- квадрат распределения с  n – 1  и  m – 1  степенями свободы соответственно.

Обычно полученные оценки различны, в связи с чем возникает вопрос, можно ли на основе обработки экспериментальных данных полагать, что  =  (нулевая гипотеза).

Если нулевая гипотеза справедлива, то это означает, что выборочные дисперсии (7.2.8) представляют собой оценки одной и той же характеристики рассеивания генеральной совокупности и их различие определяется случайными причинами. В противном случае различие оценок существенно и является следствием того, что дисперсии генеральных совокупностей различны.

В качестве показателя согласованности гипотезы о равенстве дисперсий примем отношение большей оценки дисперсии к меньшей. Для определённости будет полагать  > , тогда