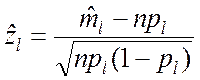Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

                                                .                            

Нормированные случайные величины  связаны между собой линейным соотношением

                           .       

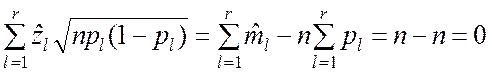На основании этого утверждаем, что случайная величина 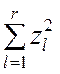 будет приближённо следовать хи-квадрат (c²) распределению. Если эту случайную величину принять за показатель согласованности гипотезы, то получим равенство

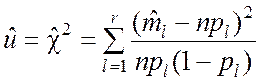                                            .              (7.1.9)

Преобразуем выражение (7.1.9), учитывая, что

                                                      

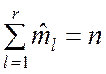
и 1– p_l » 1 при больших значениях n:

                                 (7.1.10)

или

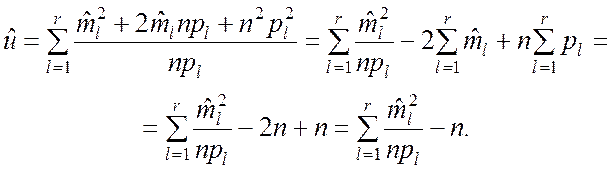                                                                           (7.1.11)

Выражения (7.1.10) или (7.1.11) используются в зависимости от формы представления результатов наблюдения, т.е. в зависимости от того, являются ли исходными данными  или m_l.

Как известно, распределение c² зависит от числа степеней свободы f = r – s,  равного числу интервалов r минус число независимых условий (связей), наложенных на частоты . В формуле (7.1.10) предполагается наличие только одного условия

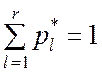                                                       ,                        (7.1.12)

которое накладывается всегда. Тогда принимаем s = 1 и число степеней свободы  f = r – 1. Равенство (7.1.12) есть сумма вероятностей несовместных событий, образующих полную группу.

В случае, когда теоретическое распределение подбирается так, чтобы совпадали его математическое ожидание и оценка математического ожидания, полученная по результатам наблюдения, т.е.

                                                    ,                                

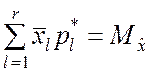число связей увеличивается на единицу. Следовательно, s = 2  и число степеней свободы  f = r – 2. Если условие совпадения параметров теоретического и статистического распределения распространяется и на дисперсию

                                             ,                         

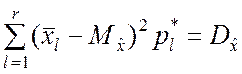то s = 3,  f = r – 3  и т.д.

Таким образом, число степеней свободы распределения c² зависит при проверке гипотез от условий проведения проверки, что необходимо учитывать, используя показатель согласованности гипотезы (7.1.13) или (7.1.14).

Можно показать, что при невыполнении гипотезы H₀ по мере возрастания n значение показателя согласованности  будет неограниченно увеличиваться, т.е. кривая распределения  сдвинута относительно кривой  вправо. Поэтому в соответствии с рекомендациями предыдущего раздела в качестве критической целесообразно выбрать правостороннюю критическую область, рис.7.3.

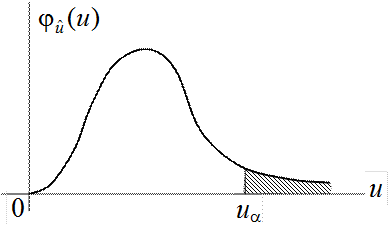
Рис.7.3. Правосторонняя критическая область

В этом случае для определения критической границы u_a можно использовать приложение 7, в котором даны критические точки распределения c² в зависимости от уровня значимости a и числа степеней свободы  f.

Порядок проверки гипотезы о виде закона распределения состоит в следующем.

1. Назначается уровень значимости a, и по таблице критических точек распределения c²  (приложение 7) определяется критическая граница u_a. Входами в таблицу служат уровень значимости a и число степеней свободы  f.

2. Результаты эксперимента представляются в виде интервального статистического (вариационного) ряда (табл.4.5), в котором m_l и  – число и частота попаданий исследуемой величины  в l-й интервал () соответственно.

3. Вычисляются вероятности p_l попадания случайной величины , которая подчиняется гипотетическому закону распределения, в l-й разряд:

                                   ,               

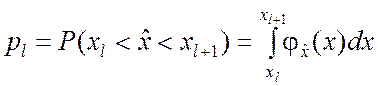где  – плотность распределения гипотетического закона. Очевидно, что должно выполняться условие

                                                       .

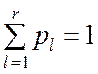4. Рассчитывается значение u показателя согласованности гипотезы по формуле (7.1.10) или (7.1.11).

5. Проверяется условие u £ u_a. Если оно выполняется, то расхождение между экспериментальными данными и гипотезой H₀ полагается незначительным. В противном случае нулевая гипотеза отвергается.