Методы проверки гипотез о законах распределения и параметрах законов распределения (Раздел 7 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 9

П р и м е р 7.5. При исследовании стабилизатора напряжения проведено семь испытаний и получена оценка дисперсии выходного напряжения, равная 0,06 B². После доработки стабилизатора проведено ещё 13 испытаний, в результате чего оценка дисперсии выходного напряжения стала равна 0,10 B². Есть ли основание полагать, что в результате доработки точность стабилизатора не изменилась?

▼ Обозначим  = 0,10 В²,  = 0,06В². Тогда n = 13, m = 7. Задаёмся уровнем значимости   a = 0,10  и  в  приложении  5  находим  u_a2  для  a/2 = 0,05,   f₁ = n – 1 = 12,   f₂ = m – 1 = 6.  Также находим  u_a1  для a/2 = 0,05,   f₁ = m – 1 = 6,   f₂ = n – 1 = 12.   Получаем    u_a2 = 4,  F_(0,05;6;12) = 3  и,  следовательно,   u_a1 = 0,33.

Значение показателя согласованности по формуле (7.2.11):

                                             .

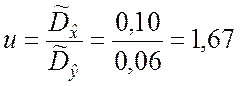Так как u_a1 < u < u_a2, то гипотеза H₀ о том, что доработка не повлияла на точность стабилизатора напряжения, принимается.                ▲

2. H₀: = ;     H₁: > .

В этом случае строят правостороннюю критическую область таким образом, чтобы вероятность попадания в эту область показателя согласованности в предположении о справедливости нулевой гипотезы была равна принятому уровню значимости:

                                                   .

Критическую точку  находят по таблице критических точек  распределения  Фишера, используя в качестве  аргументов  a,  f₁ = n – 1,   f₂ = m – 1. Наблюдаемое значение показателя согласованности определяется по формуле (7.2.11). Если u < u_a, то нет оснований отвергнуть нулевую гипотезу, в противном случае она отвергается.

3. H₀:  = ;    H₁:  < .

В данном случае строят левостороннюю критическую область таким образом, чтобы

                                                   .                               

Критическая точка находится по таблице критических точек распределения Фишера на основе отношения

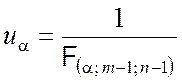                                     .                                        (7.2.12)

В знаменателе (7.2.12) – табличное значение, найденное при аргументах  a,  f₁ = m – 1,   f₂ = n – 1.

Наблюдаемое значение показателя согласованности определяется по формуле (7.2.11). Если u > u_a, то нулевая гипотеза принимается, в противном случае она должна быть отвергнута.

В заключение следует отметить, что показатель согласованности гипотезы (7.2.9) можно использовать для сравнения дисперсий и в том случае, когда для одной из дисперсий найдена не оценка, а её точное значение. В этом случае число степеней свободы закона распределения Фишера в числителе или знаменателе выражения (7.2.9) следует устремить к бесконечности, в остальном методика проверки гипотезы остаётся прежней.

П р и м е р 7.6. Из партии снарядов с известной характеристикой рассеивания по дальности  испытываются 10 снарядов, хранившихся без специальной тары. Есть ли основание полагать, что по причине такого хранения рассеивание снарядов по дальности возросло, если в результате испытаний получена оценка ?

▼ В данном примере кривая распределения характеристики  при конкурирующей гипотезе смещена влево, поэтому в качестве критической выбираем левостороннюю область.

Пусть a = 0,05, тогда для определения u_a входим в таблицу приложения 5  со  значениями    a = 0,05,   f₁ = m – 1 = 9,   f₂ = ¥.  Получим F_(0,05;9;∞) = 1,88, следовательно,

                                                 .                             

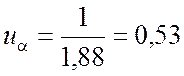Вычисляем значение показателя согласованности

                                            .

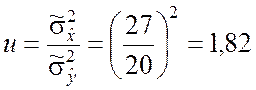Так как u > u_a и значение показателя согласованности попало в область допустимых значений, то нет оснований утверждать, что в результате хранения без специальной тары рассеивание снарядов по дальности возросло.

                                                                                                              ▲