Системы реального времени. Технологические процессы. Функции АСУ ТП в реальном времени. Информационный подход. Модели и алгоритмы управления, страница 5

Основным источником погрешности измерений является АЦП .

                                                  q =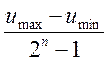

Зная вторую производную, можно еще улучшить алгоритм отбраковки.

Алгоритм с использованием производных требует, чтобы предыдущие отсчеты были не искажены. Для алгоритма с первой производной самый первый отсчет должен быть получен  с  max   точностью, если используется вторая производная, то два  первых отсчета должны быть точными. Для этого в начале работы алгоритма в момент    t₀    производят многократный опрос  с усреднением каждого сигнала (датчика).

2. Спектральный подход

Допустим, что:

x₁ -  сигнал /информация, определенная на отрезке времени  (t₀; t₀ + Т ), где Т – период/время наблюдения.

                                                 x₁(t) = x(t) + ω(t),

где  x(t) – идеальное значение сигнала,

ω(t) – помеха/искажение сигнала.

                                                            ≤ ξ

Допустим с ЭВМ получаем :

N_x – число, пропорциональное  x_i(t) в ЭВМ – отчет x₁.

Частотный метод отбраковки основан на предварительном изучении сигнала  x(t), анализе этого сигнала и определении спектра S_Х

S_Х – спектр x(t) на отрезке (t₀; t₀ + τ).

Если  полученный новый отсчет N_х после анализа на спектральную характеристику не укладывается в полученный ранее спектр S_Х, то такой отсчет N_x бракуется и заменяется предыдущим неискаженным.

Статистический метод отбраковки

 Отбраковку ложной информации при вводе ее в ЭВМ можно производить, используя известные методы математической статистики. Для отбраковки грубых ошибок измерений можно воспользоваться статистическим критерием Смирнова, который основан на гипотезе о нормальном законе распределения ошибок измерений.

Критерий Смирнова

Высчитывается величина    ξ    – статистика, которая определяется следующим образом:

                                                     ξ = 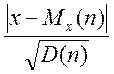                                                                 (4)  

ξ – статистика,

x – измеренный отсчет,

M_х(n) – математическое ожидание(среднее значение),

D(n) – дисперсия,

n– количество степеней свободы/количество измерений величины   x,    по которым измеряется

М    и   D.

Вычисляется статистика по (4) и сравнивается с критическим  значением ξ_кр(р) и затем  относят полученное значение x /результат измерения к грубой ошибке  с вероятностью   p.

p – вероятность отнесения к грубой ошибке.

Фильтрация  случайных помех(шумовые)

Методы фильтрации сглаживания случайных помех занимается  борьбой с постоянно присутствующими искажениями шумового характера, амплитуды которых распределены по нормальному закону.

1. Экспоненциальное сглаживание.

 Алгоритм экспоненциального сглаживания основан на учете влияния предыдущих значений сигнала на его последующую реализацию. Алгоритм достаточно прост, сложность заключается в подборе коэффициентов.

Алгоритм:

   (n) = γ_x ·x(n) + (1 – γ_x) · (n-1)                                                                               (1)  – это уравнение является  дискретным вариантом ДУ – I

Оно  отражает влияние предыдущего сигнала на последующий.

x(n)  - значение сигнала, снятого с АЦП в момент времени (n)

n – дискретное время: n = 0,1,2…(N - 1)

Т = t_n – t_o;            = N – число дискрет за время (Т) наблюдений

,   – сглаженные значения сигналов в момент времени (n) и (n– 1)

γ_х – коэффициент  экспоненциального сглаживания.

Свойство сигнала, т.е.     x(n),   и помехи в этом сигнале  отражаются в значении коэффициента  γ_х

Коэффициент γ_х определяется путем моделирования исследованного сигнала и подборе величины γ по критерию  min  остаточного шума.

Реально коэффициент

Метод оптимальной фильтрации

Если есть возможность исследовать свойства сигнала, а также влияние помехи, то наилучшие результаты фильтрации случайных помех дает метод оптимальной фильтрации.

     Схема этого метода: