Системы реального времени. Технологические процессы. Функции АСУ ТП в реальном времени. Информационный подход. Модели и алгоритмы управления, страница 10

Математическое описание непрерывных процессов.

Задача идентификации

Математическое описание непрерывных процессов имеет ряд особенностей, к которым можно отнести следующее: многофакторность, плохую организацию внутренней структуры, что определяет нечеткое проявление причинно-следственных отношений, распределенность целевых функций во времени и в пространстве, нестационарность свойств и параметров.

Под моделью будем понимать некоторый оператор R.

Модель R характеризуется 2-мя основными характеристиками: структура St

и параметр , т.о., R=<St; >

Идентификация

Идентификацией, в широком смысле, называется процедура определения структуры и параметров модели, обеспечивающих наилучшее совпадение всех координат модели и объекта при одинаковых входных условиях.

Сам процесс идентификации можно изобразить следующим образом:

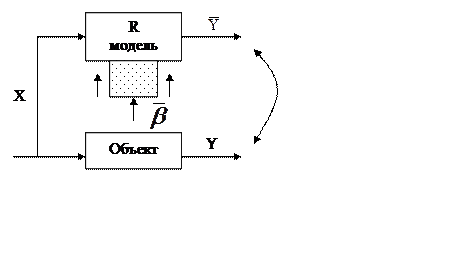Из определения – основные этапы процедуры идентификации:

1)  Выбор структуры (структурный синтез). St -?

2)  Выбор критерия близости объекта и модели, основанный на специфике задачи моделирования. J - ?

3)  Определение вектора параметров =(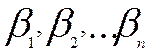), оптимальных с точки зрения выбранного критерия близости.

4)  R=. Проверка адекватности модели / признаков окончания процессов идентификации.

Если в результате п. 4 есть неудовл. модели, то надо возвратиться к п. 1.

В процессе идентификации / получения модели используются исходные данные 2-х типов: априорная информация, на основе которой выбирается структура модели, т.е представление об операторе R; апостериорная информация, полученная в процессе наблюдения за объектом, т.е. мы имеем наблюд. За X и Y  I=<X,Y>, иначе такие наблюдения называются временными рядами, т.е. временной ряд – это последовательность значений входных и выходных координат, полученных через определенный заданный промежуток времени ∆t.

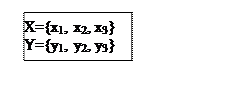
Совместно полученные данные, т.е.

Структурный синтез модели

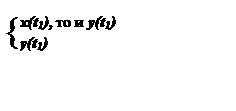
Под моделью объекта будем понимать правила преобразования воздействия на объект X в реакцию объекта Y, т.е. X→Y.

В простейшем случае модель представляет собой зависимость между скалярным значением x и y, т.е.  

модель y=f(x)

1) Самый простой вариант модели: y=kx+b                                                                                                                        (1)

k,b→

2) Более сложный вид модели, которая отражает реакцию в виде функционала:

y=Ф{x(t)}                                                                                                                        (2)

Преобразование функции в число-функционал:

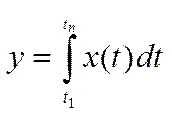
С помощью функционала определяют критерии.

3) Оператор преобразования одной функции в другую:

y(t) = R{x(t)},                                                                                                                             (3)

где R –оператор.

Самый простой оператор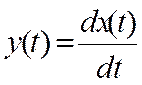                

Т.о., синтез модели – это определение зависимости между входной и выходной функциями.

Под синтезом внешней структуры понимают определение количественного состава координат, поддающихся наблюдению за объектом.

Декомпозиция модели

- это разделение сложной модели на более мелкие ее составляющие.

Критерием декомпозиции модели может служить:

·  необходимость определения промежуточных координат;

·  разделение сложных процессов на параллельные процессы;

·  наличие у объекта перекрестных связей.

На рисунке показан пример наличия у модели перекрестных связей.

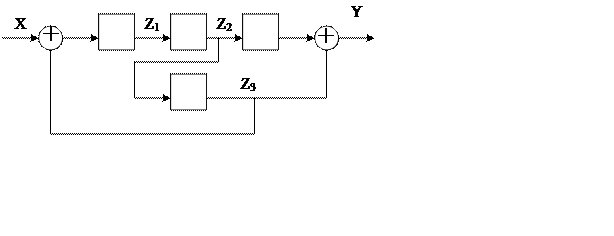После декомпозиции для идентификации мы должны представить следующую модель:

R: X=>Y/XCQ^m, YCSⁿ

Y* - идеальное значение выхода;

F – воздействие внешней среды;

R – оператор;

m,n – размерность входных и выходных координат.

Физико-химические модели

Первым вариантом построения модели должны быть физико-химические модели, определяющие поведение физических и химических процессов.