 Эта градуировочная характеристика может
задаваться в различном виде, но самая удобная для нас – это аналитическая
запись
Эта градуировочная характеристика может
задаваться в различном виде, но самая удобная для нас – это аналитическая
запись
Второй вариант записи характеристики: табличный
|
P |
P1 |
P2 |
… |
PN |
|
UД |
U1 |
U2 |
… |
UN |
Кусочно – линейная зависимость:
Если для нас задано аналитическое выражение для градуировочной характеристики, то при пересчете сигнала необходимо найти обратную характеристику:
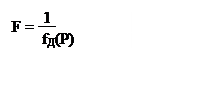 UД = fД (P)
UД = fД (P)
↓
P = F (UД)
UД ≈ NД
Если градуировочная характеристика задана таблично, то по этой таблице необходимо получить аналитическое значение градуировочной характеристики, т.е. провести аппроксимацию точечно заданной функции. Для этой цели, чаще всего, используются степенные ряды.
Допустим на входе мы имеем некоторую величину: Nx – число, полученное в результате вычислений ЭВМ. Аппроксимирующую функцию можно представить следующим степенным рядом:
x = ax0 + ax1Nx + ax1Nx2 + … + axkNk (2)
ax , ax1 ,…, axk - коэффициенты разложения в степенном ряду,
k – старшая степень степенного ряда.
Для получения аналитического выражения для степенного ряда необходимо знать коэффициенты разложения от k0 до kk и величину k. Коэффициенты определяются методом наименьших квадратов. Если характеристика датчика задана графически:
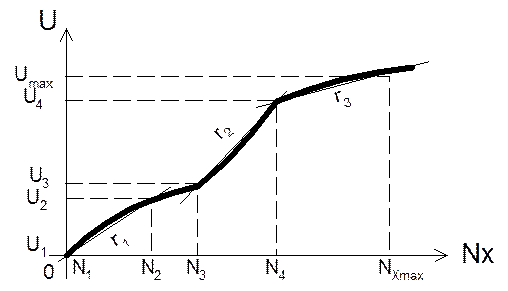
для нахождения аналитического вида можно воспользоваться методом кусочно-линейной аппроксимации. Вся кривая при этом разбивается на m – линейных участков.
Значение сигнала x определяется следующим выражением:
x = Mx,r · Nx + Nx,r (3),
Nx Î [ ax,r , bx,r] ; r = 1,2,… ,m (4)
Mx,r и Nx,r - это константы.
Для вычисленной величины Nx определяют, в какой из участков аппроксимации попала данная величина, используя (4). В памяти ЭВМ находятся значения Mx,r и Nx,r , которые берут и подставляют их значения в выражение (3).
Коэффициенты Mx,r и Nx,r определяют из графика аппроксимации кривой.
В результате полученных вычислений были рассмотрены три основных подхода для преобразования вычисленных значений в их реальное значение. Эти значения и выводят в качестве физических величин для оператора.
Теория Котельникова.
Если в спектре сигнала нет частот выше чем wmax, то такой сигнал с достаточной точностью можно восстановить, если его преобразовывать с периодом / шагом по времени

∆T ≤ π / wmax = 1/ 2fmax - теоретическое значение, т.е. теоретически предел меньше которого брать нельзя.
∆Tпрактически ≤ π / 4÷6 wmax = 1/ 8÷12 fmax
Рассмотрим второй подход
Временной подход (амплитудный)
![]() x(t)Если задаться ошибкой по амплитуде
x(t)Если задаться ошибкой по амплитуде
![]() ε ε – ошибка
преобразования амплитуды
ε ε – ошибка
преобразования амплитуды
![]()
![]()
![]()
![]()
![]()
![]()
 x(t)
ΔT
– шаг дискретизации
x(t)
ΔT
– шаг дискретизации
![]()
![]()
![]()
![]() fmax(
fmax(![]() )
)
![]()
|
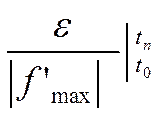
![]()
![]()
![]()
![]() Δt Δt ε = ξ (кси)
Δt Δt ε = ξ (кси)
![]()
![]()
![]()
![]() ΔT
ΔT
![]() t
t
![]() t0
tn
t0
tn
[f ' max] – модуль max скорости изменения сигнала / информации
tn – to = Т – период / время наблюдения
Отбраковка ложной информации
Искажение информации при ее передаче во времени и пространстве, а также при преобразовании информации из одного вида в другой, обязательно присутствует искажение.
Истины мы не знаем никогда!
Всевозможные искажения информации делятся на два вида :
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.