1. Редкие по времени, но большие по амплитуде (величине искажения данных). Такие искажения называют ложной информацией (импульсной помехой). Модель этих искажений выглядит следующим образом : амплитуда – это Δ функции (т.е.= ∞) , частота возникновения, описанная Пуассоновским законом.
 |
![]()
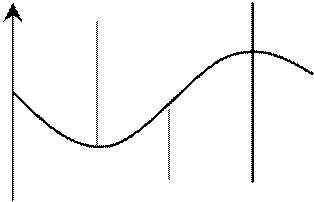
2. Постоянно-текущие искажения шумового характера, математической моделью является нормальный закон распределения с нулевым математическим ожиданием и ограниченной дисперсией.
 |
Реально мы имеем сумму искажений и
![]() того и другого характера.
того и другого характера.
Рассмотрим поочередно искажения.
1. Отбраковка грубых искажений.
![]() 1.
Первый подход отбраковки – амплитудный подход.
1.
Первый подход отбраковки – амплитудный подход.
![]() x
x
![]()
![]()
![]()
![]()
![]()
![]()
 ξ
ξ
![]()
![]()
![]()
![]()
![]()
![]()
![]() b
b
![]() xi
xi
![]() a
a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ξ
ξ
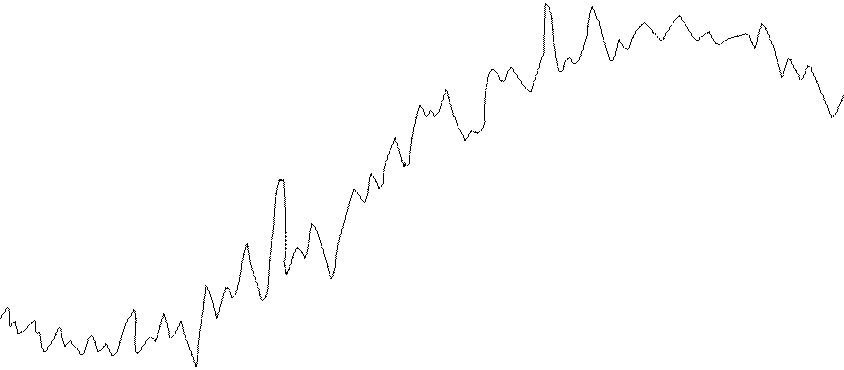
t0 t1 t2 t3 t4 t6 t9 tn t
x̃(t) – идеальное (точное) значение непрерывного сигнала
![]() (
) - накладывающиеся искажения
(
) - накладывающиеся искажения
![]() –
то значение сигнала, которое мы получили после преобразования в
вычислительной
машине.
–
то значение сигнала, которое мы получили после преобразования в
вычислительной
машине.
xi = xi (ti) – преобразованное значение х(t) в ЭВМ
Простейший случай отбраковки информации основан на известных характеристиках амплитуды сигнала.
Допустим,
известно, что реальный сигнал a ![]() x̃ (t) ≤
b
x̃ (t) ≤
b
а – min значение х̃; b – max значение х̃ ,
ξ – точность преобразования.
Алгоритм
I шаг
Если известно,
что a ![]() x̃ (t) ≤ b
(1) и определено, что модуль разности
x̃ (t) ≤ b
(1) и определено, что модуль разности ![]() ≤ ξ
(2) / (1) и (2) – исходные данные /
≤ ξ
(2) / (1) и (2) – исходные данные /
, то значение xi для которого не выполняются следующие равенства:
a – ξ ≤ xi ≤ b + ξ (3)
бракуется и заменяется предыдущим неотбракованным значением.
Учтем ограниченную скорость изменения сигнала внутри заданного изменения амплитуды (a,b)
II шаг
Пусть известно, как и раньше a ≤ x̃ ≤ b .
Также
известно, что скорость изменения сигнала лежит в пределах c ![]()
![]() (t) ≤ d, где
(t) ≤ d, где ![]() - производная, причем d =
- c . Измерения производим с точностью ξ. Т.е.
- производная, причем d =
- c . Измерения производим с точностью ξ. Т.е. ![]() ≤
ξ
≤
ξ
Если не выполняется хотя бы одно из следующих неравенств
a – ξ ≤ xi ≤ b + ξ
c · ![]() – 2ξ ≤ (xi – xi) ≤ d ·
– 2ξ ≤ (xi – xi) ≤ d · ![]() + 2ξ
+ 2ξ
(2ξ , так как ошибки складываются ξ у xi и ξ у yi → ξ+ ξ=2 ξ)
то такое значение xi бракуется и заменяется предыдущим неискаженным значением.
![]() (t) =
(t) = 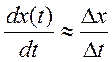 при t→0
при t→0
![]() ΔT = ti – ti-1
ΔT = ti – ti-1 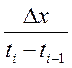 = (
= (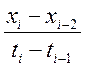 )
)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.