Другие предметы \ Системы реального времени

Системы реального времени. Технологические процессы. Функции АСУ ТП в реальном времени. Информационный подход. Модели и алгоритмы управления, страница 14

Заданы длительности произведения всех этапов каждой работы τ i,j,k , где : i – номер работы; j – номер участка; k – номер линии внутри участка. И заданы условия -  ограничения, определяющие специфику отношений между операциями в рамках рассматриваемого технологического процесса.

 Требуется составить план проведения работ, минимизирующий полное время занятости производственной системы .

Время занятости от времени начала первой работы до окончания последней работы.

Причины отсутствия общего решения заключается:

1. Сложность структуры расписаний, дискретность, многовариантность.

2. В отсутствии необходимого условия экстремума функционала Тс.

Выбор критерия.

1. Минимум времени занятости системы:

2. Минимум суммарной величины простоев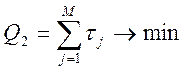

где  τj - время простоя j-того оборудования.

3. Максимум выпуска в стоимостном выражении

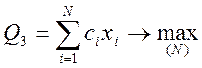
Где      ci - стоимость произведенной работы;

            xi - объем i-того продукта.

4. Максимум прибыли

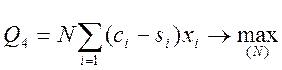
Где      ci - стоимость;

            si - себестоимость;

            xi- объем i-того продукта/услуги.

Если трудоемкость и себестоимость зависят от  объема продукта, то есть от объема i-того продукта/услуги, то расчет критерия ведется для зон допустимой стабильности этих показателей.

План работ может изображаться в двух различных формах.

1. Матричная форма.

2. График Ганта.

Матричная форма описания задачи.

1. Задается совокупность технологических операций G

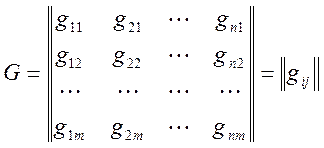
     нет операции

                         операция выполняется

Где      n - работа

            m - операция

2. Пооперационная трудоемкость:

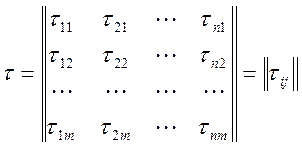
где      i – номер работы

            j – номер этапа.

3. Решение задачи определяется либо в виде матрицы планов P, либо матрицы моментов (T).

Матрица планов:

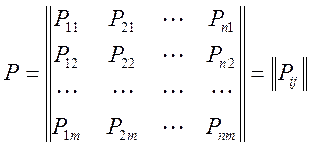
Где Pij  - порядковый номер выполнения i-той работы на j-том этапе участия.

Матрица моментов:

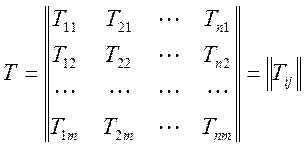
Где Tij – определяет моменты начала выполнения i-njq работы на j-том этапе участке.

Постановка и формирование задачи планирования работ

производственной системы (упрощенный вариант)

Постановка:

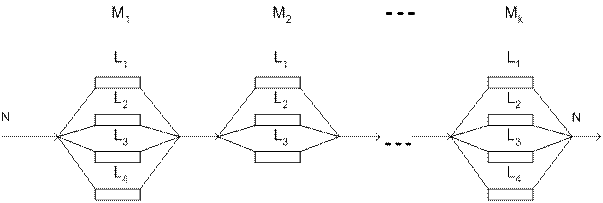
Пусть задана производственная система, объединяющая M- одноканальных участков/этапов, каждый из которых характеризует вполне определенный этап ТП.

M(1) – M одноканальные участки.

Имеется N – работ выполняемых с/силой в некоторой последовательности. Известно и фиксированная норма времени τij, где i-N работа, j-N участка/этапа.

Введены ограничения:

1. Очередность работ сохраняется на всех участках неизвестной.

2. Момент начала j-того этапа i-той работы не может наступить раньше момента окончания (j-1) этапа той же работы.

3. Для отдельных работ установлены плановые сроки окончания, которые необходимо выдерживать. Tiп

4. Возможна частичная упорядоченность работ.

5. Могут быть ограничения приоритетного характера.

Требуется в заданных условиях определить последовательность проведения работ, наилучшую в смысле минимума времени занятости системы

График Ганта.

График Ганта это, фактически,  временная диаграмма выполнения работ:

T1 – время работы (всей первой работы по всем этапам)

t0 = 0 время начала отсчета;

t0j = момент возможного начала j-того этапа первой работы;

Δt01 = время подготовки;

τ21 = вторая работа первого этапа;

Δti-1j = время задержки начала j-того этапа i-той работы, все дальнейшие математические выражения вытекают из ограничений заданной постановкой  задачи;

Δti-1j≥0

Учитывая условия б) , которое определяет моменты начала j-того этапа  i-той работы и тому подобное. Это условие можно формализовать (математически описать) следующим образом:

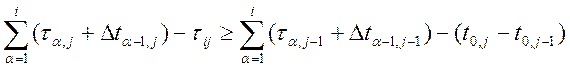                                   (1)

Для того, чтобы перейти от неравенства к равенству введем переменную вспомогательную:

Θij; Θij ≥ 0 и подставить в формулу (1), получим следующее:

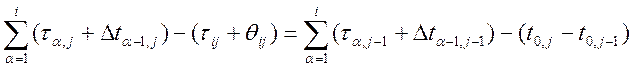                        (1)'

Скачать файл