Системы реального времени. Технологические процессы. Функции АСУ ТП в реальном времени. Информационный подход. Модели и алгоритмы управления, страница 15

Из выражения (1)' можно определить время, за которое должна быть выполнена i-тая по порядку работа:

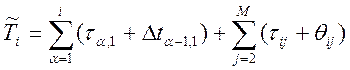                                                                        (2)

Объединив номера i-той работы, для которых определены плановые сроки – множество Sп (п – плановая), может получить формальное выражение для условия в) из формулы (2)

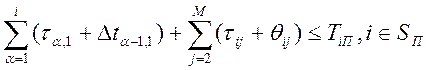                                                           (3)

Приведем выражение 3 для плановых сроков к равенству, введя вспомогательную переменную φ_ni; φ_ni≥0. Подставив φ_ni в 3., получим следующее:

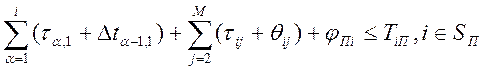.                                                 (4)

Условия а), г), д) (очередность работ сохраняется) связывают порядковые номера работ, которые они получают в результате подбора варианта. Формализация этих условий для нас ничего  не дает, и они используются чисто алгоритмически, то есть, если вариант не подходит, то он отбрасывается.

Проведем некоторые преобразования системы (1)', в результате, чего получаются следующее отношения:

                                                         (5)                                          

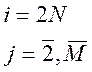
Проведем подстановку:

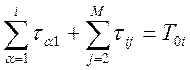                                                                                                    (6)               

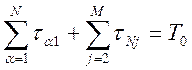
Учитывая подстановки (6), запишем оптимизационную задачу:

Постановка задачи:

Найти Θ_ij, Δt_i-1, φ_ni, доставляющие минимум следующему функционалу:

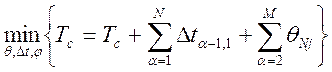при ограничениях:

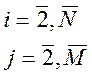                                                                                                                   (7)

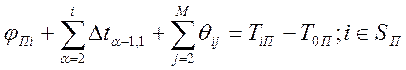
Θ_ij ≥ 0, Δt_i-1 ≥ 0, φ_ni ≥ 0                                                                                                         

Если в процессе решения задачи считать, что τ_ij = const, то данную задачу рассматривать как задачу линейного программирования, заданную в каноническом виде.

Из выражения для T_с следует, что всякое допустимое базисное решение системы (7), содержащие в числе свободных, переменные:  Δt_i-1, () и Θ_nj (), должно быть оптимизировано для данной задачи.

Основные этапы решения задачи планирования.

Данная задача состоит из двух частей:

1. Выбор варианта расстановки работ.

2. Определение для данного варианта величины времени занятости T_с в процессе решения задачи (7).

Рассмотрим первую часть.

Этапы:

1. Вводится предположение, что (N-1) позицию занимает первая по исходной нумерации работа, и исследуются варианты формирования двух последних позиций будущего плана.

1 и 2, 1 и 3, … , 1 и N            (N-1)  ←1

N-1, N

Для каждого такого варианта определяется величина Ө_ij, Δt_i-1, ω_ij и оценка времени   (8) для данного варианта.

1.1. Вводится предположение, что на (N-1) позицию установлена 2 работа и исследуются варианты.

(N-1)  ←2

2 и 1, 2 и 3,… . , 2 и N

 Для каждого из вариантов определяются значения соответствующих переменных (8).

Далее по следованию этапов повторяются подстановки до варианта, когда  (N-1)  ←N.

Все варианты упорядочиваются по принципу либо ухудшения, либо улучшения критерия T_с  и помещаются в таблицу:

Вариант
Время

2. Вводится предположение, что (N-2) позицию устанавливается первая работа и исследуются варианты трех последних мест ( N-2, N-1, N) будущего плана, причем (N-1) и N позиции, то есть продолжение процесса формировании с использованием данных предыдущей таблицы варианта. Для каждого варианта определяется переменная из формулы (8).

Все такие же операции повторяются при размещении 2, 3, … , N работ на (N – 2) позицию. Результаты упорядочиваются и сводятся в таблицу.

3.  (N-3)  ←1  и так далее.

Переход к новым вариантам продолжается до тех пор, пока не будут составлены и оценены последовательности из N- работ.

Общее число вариантов при использовании данного алгоритма не превышает N³, в отличие от N! при простом подборе.