Системы реального времени. Технологические процессы. Функции АСУ ТП в реальном времени. Информационный подход. Модели и алгоритмы управления, страница 12

G- весовая матрица (матрица весов которая определяет наше доверие к информации).

Аналитическое выражение для оценки параметров по критерию(7) зависит от вида весовой функции G.

Если матрица G определена через матрицу шумов G = F^-1, то

                                                                                        (8)

F – матрица шумов

Если G – единичная матрица, G = I, то получим оценку параметра по методу наименьших квадратов:

                                                                                         (9)

Достоинством данного подхода /одношаговой процедуры в его аналитичности. Это дает возможность вычислить не только оценки самих параметров, но и исследовать их статистичность, то есть:

1. Проверить их несмещенность

      

                                                                                                           (10)

2. Если же эти оценки сходятся по вероятности, то то они являются состоятельность:

Недостатком метода является его ограниченность, так как в общем случае модель      

может быть не аналитическим выражением, а алгоритмическим. В этом случае задачу (2) /(7) решить, аналитически не удается. В этом случае необходимо использовать другие подходы.

Многошаговые процедуры оценивания

вектора параметра β.

Данный метод основан на реализации итераций процедуры, которая формально записывается следующим образов:

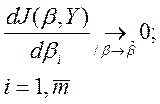                                                                                            (11)

То есть это следствие итерационных процедур по каждому из m-параметров (11.) решается для всех  m-параметров одновременно.

Процедура (11.) реализуется бесконечным числом элементов операций/шагов, с помощью которых последовательный минимальный функционал J (β) по каждому из параметров.

Минимализацию выражения (11.) реализуют численными методами, то есть, фактически алгоритмическими. В связи с этим необходимо решать: условия сходимости алгоритма, необходимой  априорной информации, кроме того, необходимо определить правило «останова»:

1. По точности вычисления параметров на i-том шаге, то есть если  β_i – β_i+1 ≤ζ, то алгоритм останавливается.

2. Количество итераций ограничено.

Реализация процедуры (11.) ограничена может быть основано на двух методах: детерминированные и стохастические алгоритмы.

Смотрим их по порядку на примерах:

1. Детерминированный метод.

1.1. градиентный метод поиска экстремума функции многих переменных.

β_i+1 = β_i ± γ_i+1*_βJ(β_i)                                                                                              (12) решается по всем m-параметрам.

β – это вектор.

Значение параметра β_i+1 = β_i ± приращение

γ_i+1 - величина шага итерации

_βJ(β_i)   - градиент (вектор для нескольких параметров β), определяется следующим образом:

γ_{i + 1} – выбирается из ряда для каждого шага : 1;1/2; 1/3;…1/i+1.

Алгоритм (12.) для линейных c/c сходится для V параметра i=0, 1, … , ∞ β(0) Чем ближе к истинным определяем мы значение параметра, тем быстрее сойдется алгоритм.

Ускорение данного алгоритма дает применение методу Ньютона.

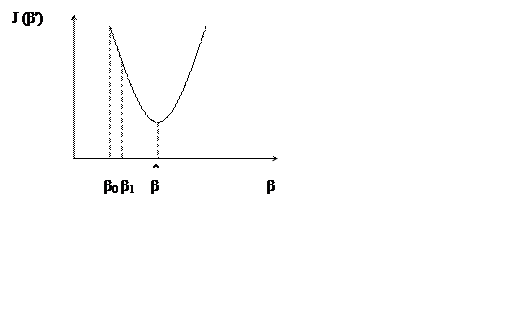
1.2. метод Ньютона

β_i+1 = β_i ± [F_β(β_i+1)]^-1 * F(β_i+1)                                                                                    (13.)

F(β_i+1)   - матрица вторых производных от функционала.

2. Стохастический алгоритм.

2.1. алгоритм стохастической аппроксимации – это модификация градиентного метода:

β_i+1 = β_i ± γ_i[_βJ(β_i) + F_i+1]                                                                                        (14.)

F_i+1 - случайные числа, как добавка к величине шага итерации.

Этот метод предлагается для немногих с/с. В этом алгоритме случайное число E дает возможность не пропустить, с одной стороны – глобальные экстремума, с другой стороны – проскочить локальные экстремумы и стационарные.

2.2. алгоритм Фабиана.