Т.о. физические и химические модели являются описанием преобразования некоторых исходных координат х в результаты химических и физических процессов. Поведение реальных объектов, в принципе, можно описывать и такими моделями. Однако подобное моделирование приводит к очень сложным соотношениям; сопряжение полученных моделей, т.е. процессов химических и физических, для реальных моделей не имеет общих законов. Поэтому моделирование систем реального времени физико-химическим моделированием не производится.
Кибернетический подход предполагает описание зависимости между входными и выходными координатами одной общей математической модели. Общая математическая модель – ядра Вольтрра, которая представляет собой бесконечную последовательность интегральных уравнений.
Для реального моделирования кибернетический подход также неприемлем из-за большой сложности получаемых моделей.
Одномерные и многомерные объекты
Под одномерным объектом понимается объект, имеющий одну входную и одну выходную координаты.
![]()
m=n=1
Если m>1 или n>1, то такие объекты называются многомерными. Для многомерных объектов необходимо иметь mхn – операторов связи.
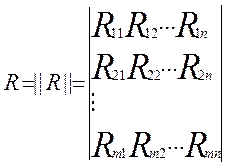 необходимо
рассматривать всевозможные связи
необходимо
рассматривать всевозможные связи
Для объекта, не имеющего перекрестные связи, размерность может быть уменьшена и объект представлен в виде следующей модели:
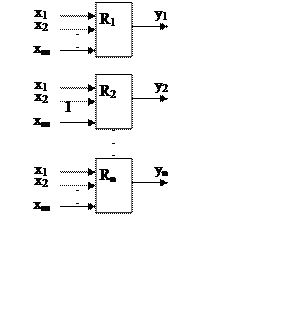
В общем случае многомерная система требует одновременной идентификации всех mxn операторов связи.
Оценивание параметров распределения
Рассмотрим процедуру оценивания параметров распределения при условии достижения экстремума функционала вида:
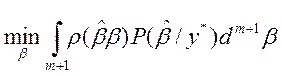 (2)
(2)
y٭ - функция потерь – значение вых. Коэффициента в (1.) экстремума.
![]() – оценка параметров;
– оценка параметров;
y* - координаты в точке ![]() minβ J (β)
minβ J (β)
1.
Квадратичная функция ![]()
Для случая квадратичной функции потерь, аналитическое выражение для параметров β будут следующими:
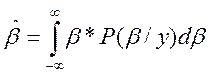 (3)
(3)
Для вычисления параметров β, используя формулу (3.), необходимы априорные данные об условном распределении параметров Р (β/y).
В результате будет получена оценка условного математического ожидания распределения параметра β.
2. Модальная
функция ![]()
В этом случае уравнение для вычисления параметра β следующие:
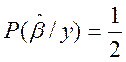 (4)
(4)
Решение уравнения (4.) дает оценку медианы апостеридной вероятности распределения параметра β.
Закономерность: при использовании различных функций потерь различается и потребность в априорной информации о распределении параметра β ковариационной матрицы, полученной из коэффициентов корреляции. При этом наблюдения возрастания требований априорной информации от оценок по методу наши квадратов до оценок произвольных функций потерь.
Оценивание параметров модели для случая разности
координат объекта и модели.
Используем условие достижения экстремума функционала вида:
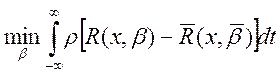 (5)
(5)
Квадратичная
функция ![]() , подставив это в формулу (5), получим
следующее:
, подставив это в формулу (5), получим
следующее:
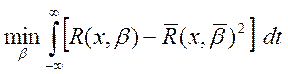 (6)
(6)
Формула (6) определяет задачи поиска параметра β, если координаты y и y – непрерываемые функции.
Если
координаты y и ![]() заданы
в дискретном виде, то есть
заданы
в дискретном виде, то есть
![]()
n – число значения выхода модели и объекта, полученные через ΔT на отрезке {tc; tn} = T
T – время наблюдения
Таким образом: n = T/ΔT, то мы получим квадратичную форму:
![]() (7)
(7)
Это дискретный аналог выражения (6)
Y – выход объекта.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.