Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ

НАПРАВЛЕНИЕ

 «ПРИКЛАДНЫЕ МАТЕМАТИКА И ФИЗИКА»

Учебно-методическое пособие.

Автоматизированные измерения и моделирование свойств

линейных систем

Составили: доц. Павлейно М.А., ст. преп. Сафронова Ю.Ф.

Санкт – Петербург

2006 г.

Содержание

Введение .........................................................................................  3

Линейные системы ........................................................................  3

Основные методы анализа линейных систем .............................  5

Системы первого порядка ............................................................  13

Системы второго порядка ............................................................  20

Применение Matlab для моделирования линейных систем .......  25

Выполнение экспериментальных измерений .............................  35

Задание к работе ............................................................................  51

Список литературы .......................................................................  51

Введение.

Целью данной работы является практическое освоение основных методов анализа линейных систем (фильтров) – временного и частотного. В первом случае задача определения сигнала на выходе фильтра решается во временной области, свойства фильтров описываются их импульсной или переходной характеристикой. Во втором случае задача решается с применением спектральных разложений. Для изучения основных особенностей применения указанных методов выбраны простейшие линейные системы – RC-фильтры первого и второго порядка. Более сложные случаи рассматриваются в работах «Резонансные явления», «Активные фильтры» и др.

Работа выполняется в два этапа. На первом этапе выполняется компьютерное моделирование линейных систем. В качестве среды моделирования используется Matlab и его пакеты расширения SignalProcessingTooldox, Simulink, SimPowerSystem.  С использованием этих программных средств строятся амплитудно-частотные, фазо-частотные, переходные и импульсные характеристики фильтров, рассчитывается прохождение через фильтры типовых сигналов.   

 На втором этапе работа фильтров исследуется экспериментально. Результаты компьютерных расчетов сравниваются с полученными экспериментальными данными. Измерения  выполняются как с использованием аналоговых, так и цифровых приборов. В последнем случае используется возможность записи данных в файл и их дальнейшей обработки в Matlab.

Линейные системы.

Под линейными понимают такие системы, параметры которых  не   зависят от величины распространяющихся  в  них  сигналов.  Строго  говоря,  любая  система  является  нелинейной,  однако  в  случае  распространения  малых  сигналов  нелинейными   эффектами,    как правило, можно пренебречь. Так, например,  сопротивление  отрезка проводника зависит от его температуры,  которая  в  свою  очередь определяется  не  только  температурой  окружающей  среды,  но  и  величиной протекающего через него тока. Последнее  обстоятельство приводит к тому, что данный объект  является  нелинейным.  Однако если величина протекающего тока достаточно мала,  то  температура проводника определяется, в основном, температурой окружающей  среды и его сопротивление практически не зависит от  величины  тока.  В этих условиях нелинейные свойства проводника можно не учитывать.

Если размеры системы достаточно малы (по сравнению с длиной волны распространяющихся в ней сигналов), то можно  не  учитывать волновой  характер  протекающих  в  ней  процессов,  в  частности излучение сигнала в окружающее  пространство,  и  ввести  понятие системы с сосредоточенными параметрами – сопротивлениями, конденсаторами и индуктивностями.  В  дальнейшем мы будем рассматривать только линейные системы с сосредоточенными параметрами.

Процессы, протекающие в линейных системах, описываются линейными дифференциальными уравнениями, которые получаются из системы  уравнений Кирхгофа для контуров и узлов. Проиллюстрируем процесс составления дифференциальных уравнений на  примере RC-цепочки, изображенной на рис.1.  

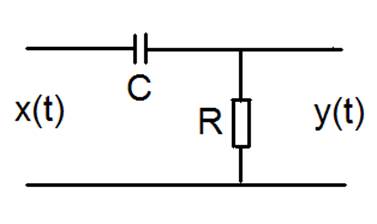
Рис. 1

Запишем уравнение Кирхгофа

или

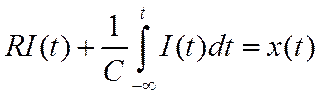
Обозначив , и продифференцировав обе части (2), получим искомое дифференциальное уравнение

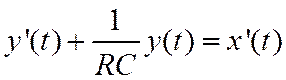
В общем случае для линейной системы с сосредоточенными параметрами дифференциальное уравнение имеет следующий вид:

Порядок дифференциального уравнения определяет порядок линейной  системы. В  частности,  рассмотренная RC-цепочка  является системой первого порядка. Заметим, что порядок дифференциального уравнения не может превышать число реактивных элементов в схеме.