Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 4

Для определения переходной характеристики нужно подать на  вход  ступенчатое воздействие ; тогда сигнал на выходе будет представлять собой функцию . На практике вместо такого входного сигнала подают прямоугольный импульсный сигнал конечной длительности, выбирая ее так, чтобы к моменту выключения сигнала можно было считать переходные процессы в цепи практически закончившимися (т.е. чтобы напряжения на всех элементах и токи через них приняли к этому времени установившиеся значения).

Чтобы экспериментально определить импульсную характеристику, нужно  подать  на  вход системы воздействие, близкое к - функции. В  качестве  критерия  "близости"  сигналов  можно выбрать критерий близости их спектров. Так как спектр - функции есть константа во  всем  диапазоне  частот,  то  для  определения импульсной  характеристики нужно выбрать такой сигнал, спектральная плотность которого неизменна  в достаточно широком диапазоне частот. Поясним это подробнее.

Пусть  нам  необходимо  определить  импульсную  характеристику фильтра нижних частот, АЧХ которого представлена на рис.4а.

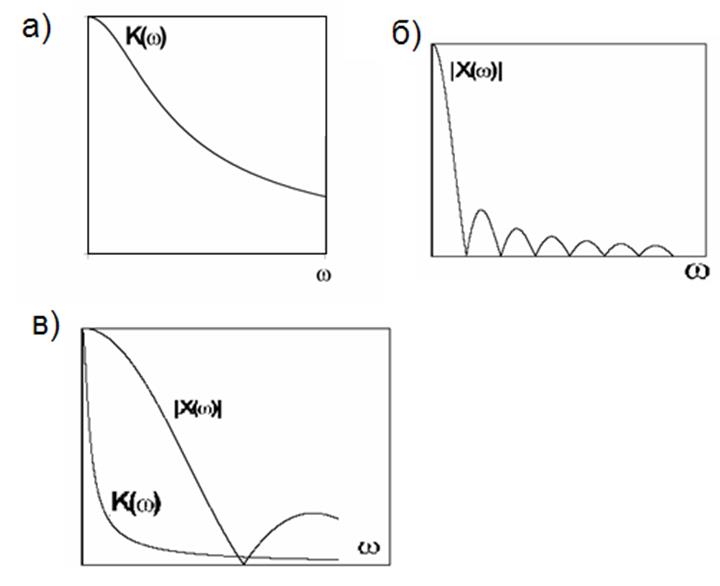
Рис. 4

Возьмем в качестве входного импульсный сигнал прямоугольной формы единичной  амплитуды и длительности. Выражение для его спектра имеет вид  (рис. 4,б).

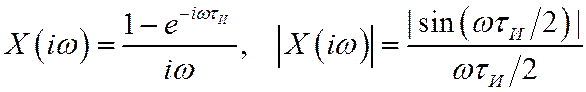
Положение первого нуля модуля спектральной функции определяется длительностью сигнала: . Если этот нуль находится по оси частот существенно дальше граничной частоты фильтра(частоты, на которой модуль коэффициента передачи  в    раз меньше максимума) (рис.  4,в), то в  полосе  пропускания фильтра спектр входного сигнала будет практически постоянным. Это означает, что такой входной сигнал  может  приближенно  считаться - функцией для данной системы, а соответствующий ему выходной сигнал – импульсной характеристикой.

Коэффициент передачи, переходная и  импульсная  характеристики  могут быть  рассчитаны  также  теоретически, на основе решения уравнения (4) с соответствующими правыми частями. Например, для определения 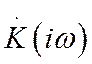, положим 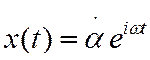. Выходной сигнал также будем искать в виде  гармонического  сигнала, но с другой комплексной амплитудой 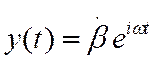. Подставив эти выражения в (4), получим

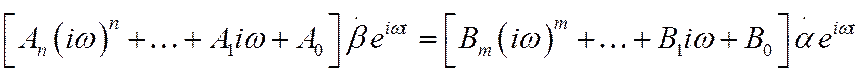
откуда получаем следующее выражение для коэффициента передачи:

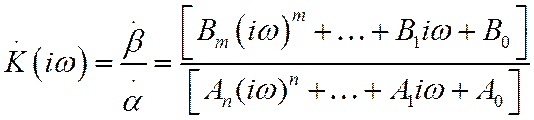
Таким  образом,  коэффициент  передачи   линейной  системы с  сосредоточенными параметрами представляет собой дробно-рациональную функцию частоты с вещественными коэффициентами. Следствием  этого является четность  АЧХ:  и нечетность ФЧХ: . Очевидно, что функция 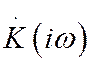не может неограниченно  возрастать  при стремлении частоты  к  бесконечности.  Поэтому  степень  полинома числителя  в  (28)  не  может  быть  больше степени полинома знаменателя. Из (28) могут быть  также  определены  переходная  и  импульсная характеристики, если воспользоваться выражениями  (23)  и (25).

Описанный  выше  способ  получения  коэффициента  передачи  не всегда  удобен,  так как требует предварительного написания дифференциального уравнения, что достаточно трудоемко для  систем  высокого  порядка.  Чаще коэффициент передачи  рассчитывают, используя символический метод. Суть его заключается в замене в схеме реактивных элементов их комплексными сопротивлениями, что упрощает определение коэффициента  передачи.

Напомним,  как получаются выражения  для  комплексных сопротивлений реактивных  элементов.  Пусть  через  индуктивность протекает гармонический ток. Тогда  напряжение на ней будет равно 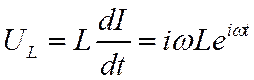. Отношение напряжения к току оказывается не зависящим  от  времени (для гармонического сигнала) и  может  быть  названо  комплексным сопротивлением индуктивности

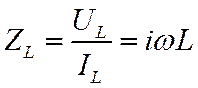
Предположим  теперь, что к емкости  приложено гармоническое напряжение . Тогда протекающий  через  нее  ток равен 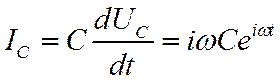   и  мы  получим следующее выражение для комплексного сопротивления емкости: