Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 7

Складывая выражения (48) и (49), получим  для  выходного  сигнала тот же результат (45), что и при решении временным методом.

Рассмотрим еще один фильтр первого порядка,  схема которого представлена на рис. 11.

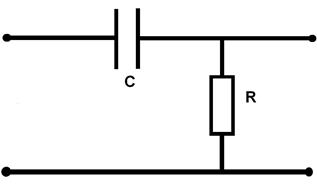
Рис. 11

Проделывая рассуждения, аналогичные приведенным выше, можно показать, что  данная  цепочка  является простейшим фильтром высоких частот (ФВЧ) с коэффициентом передачи

                                                             

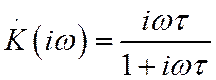
Ее АЧХ и ФЧХ описываются следующими  функциями  (рис.12):

                                                                            

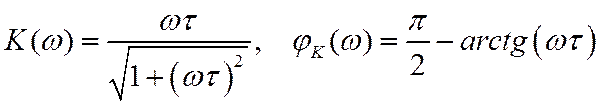
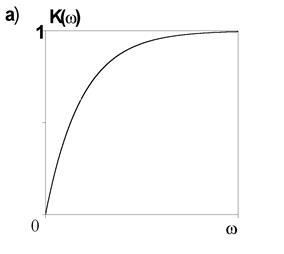     Рис. 12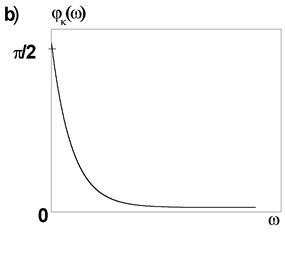     

Переходная и импульсная характеристики данной цепочки  (рис.13) имеют вид

                                             

                                     

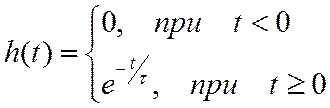
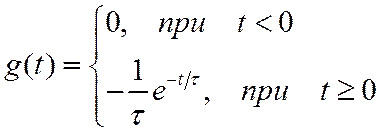
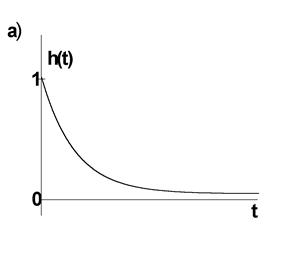    Рис. 13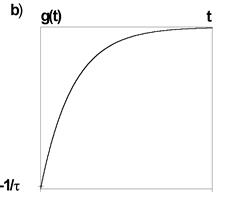    

Искажение сигнала прямоугольной  формы  при  прохождении  им  ФВЧ описываются следующим выражением:

                                   

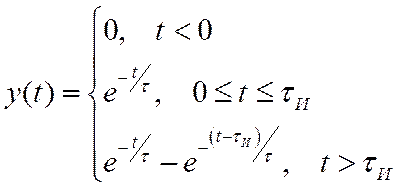
На рис. 14а изображен выходной сигнал при ,  а  на  рис. 14б – при .

        

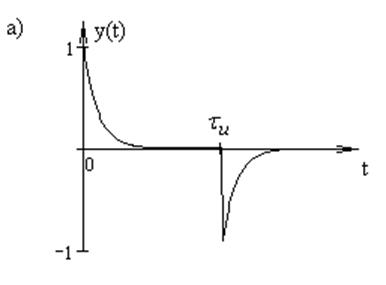
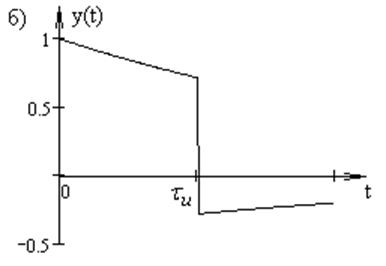
Рис. 14

Из  рисунка  видно, что длинный прямоугольный  импульс ( ) приближенно  дифференцируется  данной  цепочкой (поэтому она часто называется дифференцирующей  цепочкой).

Системы второго порядка

Выше мы рассмотрели основные свойства простейших систем первого порядка – фильтров низких и высоких частот. Рассмотрим теперь более сложную систему второго порядка – полосовой фильтр (ПФ), схема которого приведена на рис. 15.  Данный фильтр  часто  называется цепочкой Вина. Его  коэффициент  передачи  будем  искать  методом    комплексных сопротивлений:

                                                                        

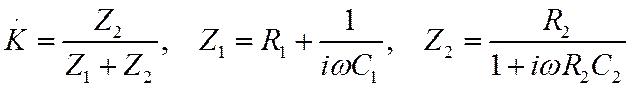
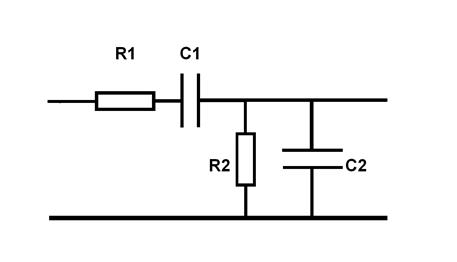
Рис. 15

Получим

                                                                                     

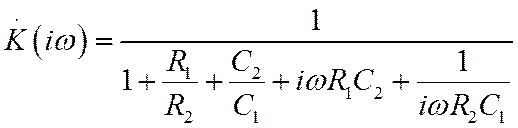
В зависимости от соотношения величин  может быть обеспечена  различная полоса пропускания фильтра. Введем обозначения , . Если  и  (симметричная цепочка Вина), то . В этом случае

                                             

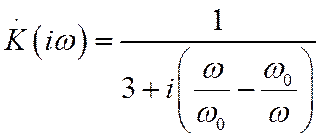
где 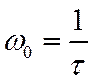. АЧХ и ФЧХ такого фильтра  описываются следующими функциями:

                                                               

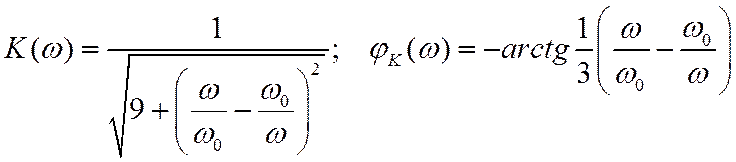
Зависимости  представлены на рис. 16.

              

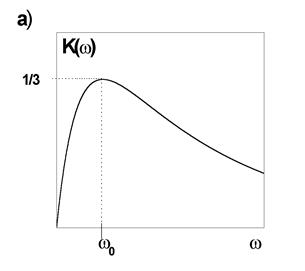
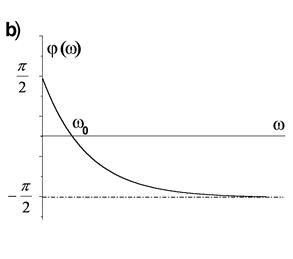
Рис. 16

При уровне неравномерности   получим следующие выражения для верхней и нижней граничных частот:

                                                                                     

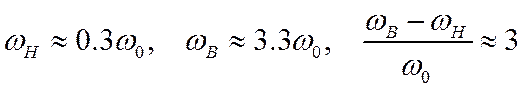
Таким  образом, при   и  мы получаем  полосопропускающий фильтр с фиксированной  относительной  полосой прозрачности.

Определим переходную и импульсную характеристики этого фильтра. Заменяя в  (57)   на  ,  запишем коэффициент передачи в виде

                                                                                     

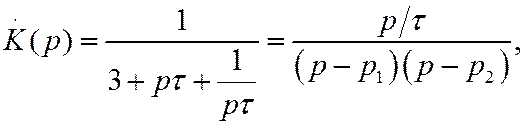
где

                                                                 

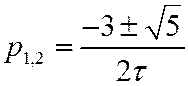
Переходная характеристика представляет собой реакцию фильтра на входное воздействие 1(t), имеющее спектр , поэтому

                                                               

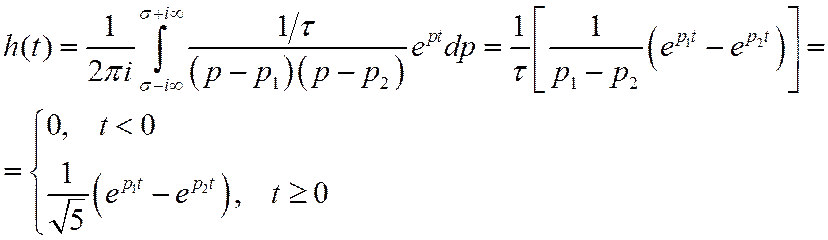
Импульсная характеристика фильтра при , в соответствии с (25), будет равна

                                           

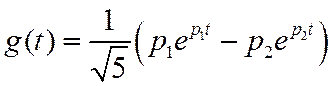
Временные характеристики рассматриваемого  фильтра  приведены  на рис. 17.

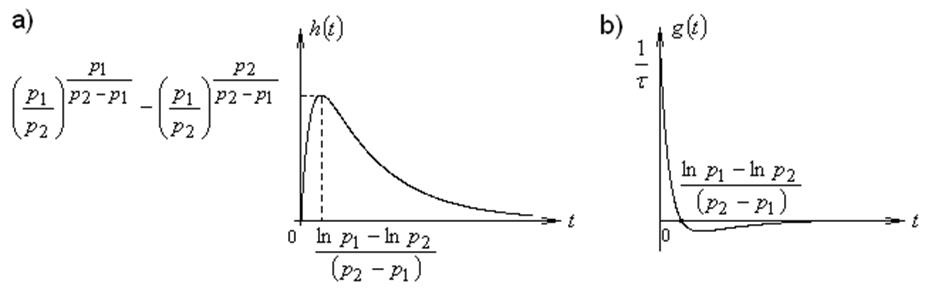
Рис. 17.

Пусть теперь

                                                       

При этом . В этом случае мы получим полосопропускающий фильтр с широкой  полосой прозрачности, относительную величину которой можно изменять соответствующим выбором параметров фильтра:

                                                                   

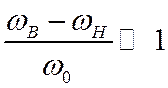
Пренебрегая  и   по сравнению с 1 в (56), получаем

                                               

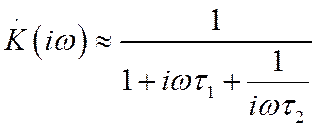
Сравнивая слагаемые мнимой части знаменателя, видим, что при  они оказываются значимы при существенно различных значениях частот. Так, на высоких частотах, где выполняется условие  , можно пренебречь третьим слагаемым в знаменателе (66), а на низких частотах при   можно пренебречь вторым слагаемым.  Поэтому можно выделить различные области частот, где на коэффициент передачи оказывают существенное влияние  постоянные времени  либо .