Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 5

                                                             

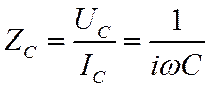
Проиллюстрируем применение данного метода на примере последовательного  колебательного  контура, считая, что входной сигнал подается на весь контур, а  выходной  снимается  с индуктивности  (рис. 5а).

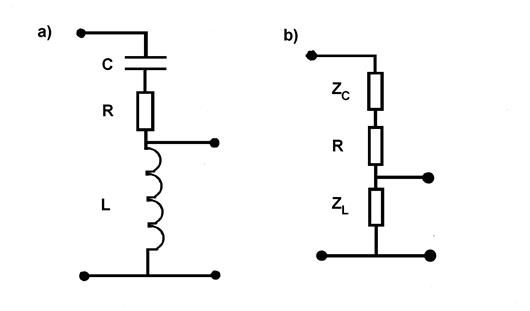
Рис. 5

После  замены   индуктивности и емкости соответствующими комплексными сопротивлениями мы приходим к схеме рис. 5б. Теперь определить коэффициент передачи совсем просто:

                                                                                   

Итак, для решения задачи о  прохождении  сигнала  произвольной формы через линейную систему с сосредоточенными параметрами можно предложить два метода.

1.  Теоретически  или  экспериментально  определить  коэффициент передачи 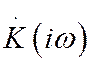  ;    рассчитать амплитуды спектральных составляющих входного сигнала   для  периодического  сигнала или спектральную функцию  для  непериодического  сигнала, воспользовавшись  выражениями  (17) или  (21),  (22),  определить выходной сигнал. В этом  случае  входной  сигнал  задается  своим  спектром, а свойства линейной системы передаются функцией частоты – коэффициентом передачи. Поэтому такой метод расчета выходного сигнала называется спектральным (частотным).

2. Теоретически  или  экспериментально  определить    переходную или импульсную  характеристику линейной системы и  с помощью выражений (8) или (11) рассчитать выходной  сигнал;  либо решить дифференциальное уравнение  (4)  непосредственно.  В  этом случае задача решается в терминах переменной ,  поэтому  такой метод называется временным.

Ниже мы рассмотрим свойства простейших RC-цепей,  используя как частотный,  так  и  временной  метод  их  анализа.

Системы первого порядка.

Рассмотрим свойства цепочки, изображенной на рис.  6а.  Применяя символический  метод  анализа, представим  эту  цепочку  в   виде делителя с комплексным сопротивлением – см. рис.6б.

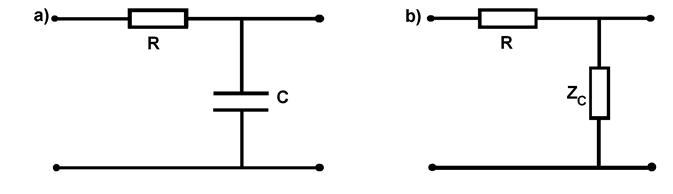
Рис. 6

Ее коэффициент передачи равен:

                                                                                    

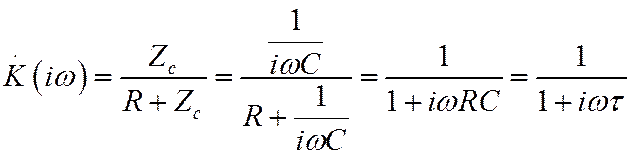
Величина   имеет  размерность  времени  и  называется постоянной времени цепочки. АЧХ и  ФЧХ  рассматриваемой  цепочки, как это непосредственно следует из (32),  описываются  следующими выражениями:

                                                                                  

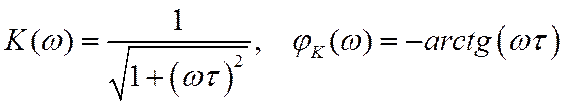
Соответствующие графики приведены на рис. 7а и рис. 7б.

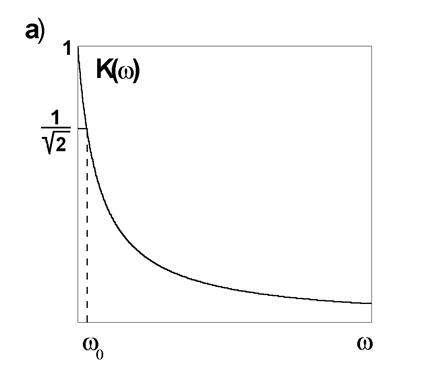
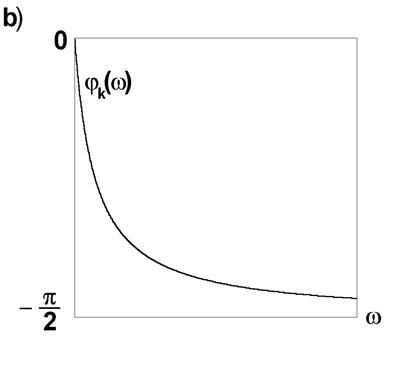
Рис. 7

Частоту ., на которой модуль коэффициента  передачи  уменьшается  в раз (чаще  всего  выбирают  ) по сравнению с максимальным значением, называют граничной  частотой. Величину  называют  уровнем  неравномерности АЧХ. Определим значение граничной частоты:

                               

Из рис. 7а  следует,  что  рассматриваемая  цепочка  представляет собой простейший фильтр низких частот  (ФНЧ):  в  области  низких частот    выполняется  условие 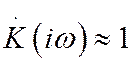, и соответствующие  гармонические составляющие входного сигнала передаются таким фильтром практически без искажения, в то время как высокочастотные  составляющие   ослабляются. Из (34) следует, что граничная частота фильтра  определяется  не параметрами и  в  отдельности, а их произведением (т.н. постоянной времени).

Заметим, что в области высоких частот коэффициент передачи приближенно описывается следующим выражением:

                                                                   

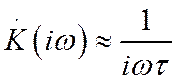
Так как умножение спектральной плотности сигнала на величину  соответствует его интегрированию  во  временной области, можно сделать следующий  вывод.  Если спектр входного сигнала, в  основном, расположен в высокочастотной (для  данного фильтра) области, то спектр выходного сигнала приблизительно равен

                                                           

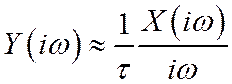
  и, следовательно, ФНЧ  осуществляет  приближенное  интегрирование этого сигнала:

                                                             

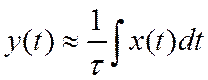
  С  этим  свойством  ФНЧ  связано его  другое название – "интегрирующая цепочка".