Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 8

Так, в области высоких частот  ()

                                         

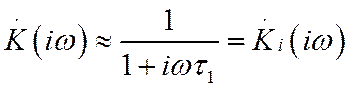
что соответствует коэффициенту передачи интегрирующей цепочки с постоянной времени . В  области  низких  частот  () получаем

                                         

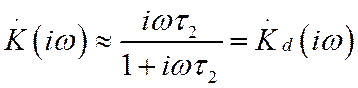
Такой коэффициент передачи имеет  дифференцирующая  цепочка  с постоянной  времени .

Для определении полосы прозрачности фильтра зададим относительный уровень ослабления АЧХ на граничных частотах следующим образом:         

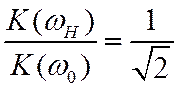
и .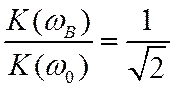

Тогда из выражений (67) и (68) получим

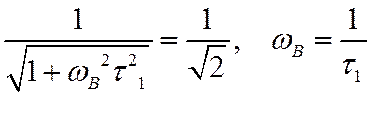                                        (69)

                                      (70)

Очевидно, что из  условия   следует, что , т.е. фильтр  – широкополосный.  Графики его АЧХ и ФЧХ приведены на рис. 18.

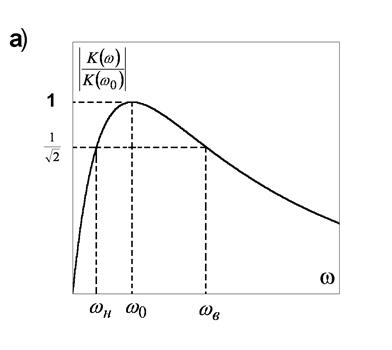     Рис. 18.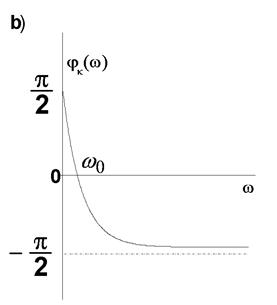   

Представим теперь выражение (66) в виде

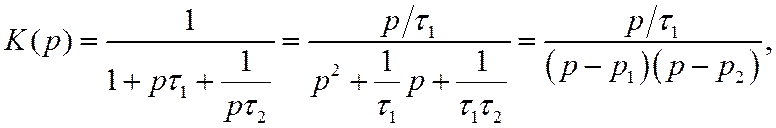                                                                (71)

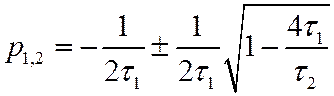где                                               (72)

Видим, что на значения корней  и  влияют оба параметра  и . Однако, учитывая неравенство , можно представить радикал в виде ряда, ограничившись двумя его членами:

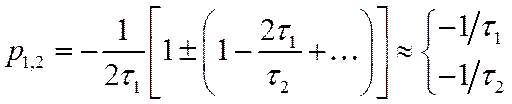                                                                                       (73)

Это дает

                                                                (74)

Формально мы получили представление выражения для коэффициента передачи фильтра  в  виде произведения коэффициентов передачи , простых фильтров, описывающих поведениеисходного фильтра в области высоких и низких частот соответственно. Подчеркнем, что это справедливо только при выполнении неравенства  . Заметим, что приближенное представление 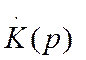 в виде (74) не означает,  что схему фильтра  можно  составить  просто  в  виде  последовательно соединенных  фильтров  с  коэффициентами  передачи   , так как при последовательном соединении нужно учитывать взаимное влияние этих фильтров.

Задания для самостоятельной работы.

1). Зная коэффициент передачи, рассчитайте переходную и импульсную характеристики данного фильтра и сравните их с аналогичными характеристиками симметричной цепочки Вина, выбирая  и , где – постоянная времени симметричной цепочки Вина. Постройте соответствующие графики. Объясните получающиеся различия.

2). Рассчитав переходную характеристику широкополосного фильтра, определите искажение прямоугольного импульса, представив  входной сигнал в виде разности двух функций единичного включения, как это  уже было сделано для ФНЧ. Постройте графики для выходного сигнала при  и .

Применение Matlab для моделирования линейных систем

Прежде чем приступать к монтажу и настройке рассчитанных фильтров, часто бывает полезно выполнить компьютерное моделирование их работы. Это позволяет устранить возможные ошибки при расчете, быстро и наглядно построить их основные временные и частотные характеристики, проследить искажение заданных входных сигналов,  оценить работу фильтров при наличии шумов. Для решения этих задач удобно воспользоваться Matlab и входящими в его состав Simulink и SimPowerSystem. Эти программные средства предоставляют широкие возможности для анализа прохождения сигналов через линейные системы.

Решать задачи, связанные с линейной аналоговой фильтрацией, можно разными способами. Во-первых, используя классические возможности написания программ в Matlab с привлечением его пакетов расширения, таких, например, как SPS Toolbox. Другой путь заключается в построении имитационных Simulink-моделей с возможным применением  SimPowerSystem. При выполнении данной работы основное внимание уделяется реализации второго подхода. Прежде чем приступить к его рассмотрению кратко напомним ряд команд Matlab, часто используемых для создания типовых сигналов и построения характеристик фильтров.

Команды, реализующие типовые сигналы:

chirp — генерация сигнала с изменяющейся частотой,

gauspuls — генерация радиоимпульса с гауссовой огибающей,

gmonopuls — генерация гауссова моноимпульса,

pulstran — генерация последовательности импульсов произвольной формы,

rectpuls — генерация одиночного прямоугольного импульса,