Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 3

                                                 

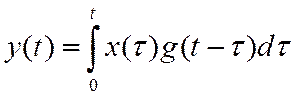
Заметим, что  как  переходная, так и импульсная характеристики линейной системы представляют собой ее реакцию на входные воздействия, равные нулю при . Следовательно, в силу принципа причинности (сигнал на выходе не может появиться раньше, чем на входе)  также равны нулю при .

Третий способ замены произвольного входного сигнала суммой стандартных воздействий основан на представлении функции рядом или интегралом Фурье. Предположим, что входной сигнал – периодическая функция с периодом T. Любой реальный периодический сигнал может быть представлен в виде ряда Фурье

                                                                                    

                                                               

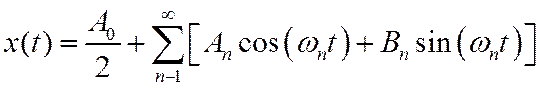
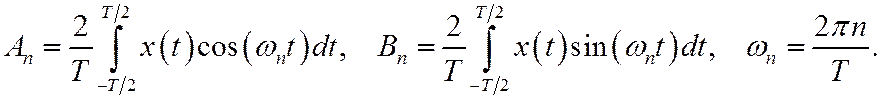
  Или в комплексной форме

                                                         

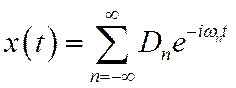
  где 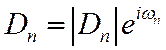   –    комплексная  амплитуда, определяемая выражением

                                                  

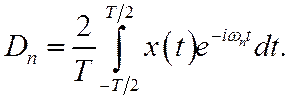
Отдельные слагаемые в рядах (12) и (14) называют гармониками.

Выходной сигнал может быть определен в общем  виде, если нам известна реакция системы на гармоническое входное воздействие при всех значениях частоты.

Пусть на вход линейной системы подается гармоническое воздействие 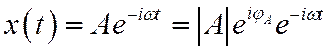 . Сигнал на выходе обозначим следующим образом: 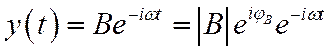.  Отношение комплексных  амплитуд  выходного и входного гармонических сигналов называется   коэффициентом передачи линейной системы

                                                                                      

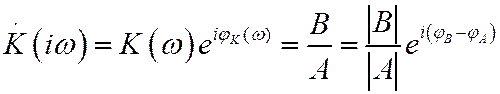
Следовательно, модуль коэффициента передачи равен отношению  амплитуды сигнала на выходе |B| к амплитуде  сигнала  на  входе   |A|,  а его фаза равна разности фаз  указанных сигналов. Зависимость   называется амплитудно-частотной характеристикой  линейной  системы  (АЧХ),  а – фазо-частотной характеристикой (ФЧХ).

Если  коэффициент  передачи  известен, то в силу принципа суперпозиции мы можем записать следующее выражение для  выходного сигнала:

                                              

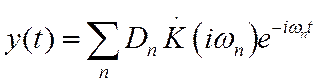
Если на вход линейной системы подается непериодический сигнал, то его следует представить в виде интеграла Фурье

                                                                       

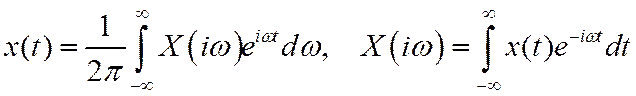
или в виде интеграла Лапласа

           .                                                               

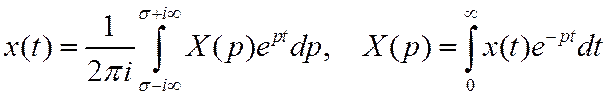Зная коэффициент  передачи,  можно  определить  спектр  выходного сигнала

                                                                     

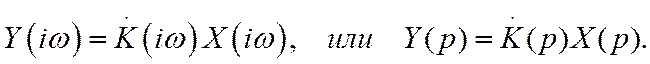
и, следовательно, сам сигнал

                                                                     

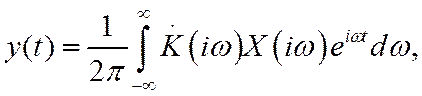
или в терминах преобразования Лапласа

                                 

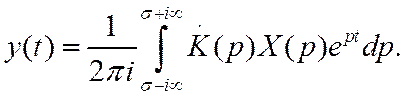
Итак,  реакция  линейной  системы  на произвольное внешнее воздействие может быть определена с помощью формул (8),  (11), (17), (21), (22), если известна переходная или импульсная характеристики линейной системы, либо ее коэффициент передачи.  Каждая  из  трех функций полностью  определяют свойства линейной системы. Очевидно, что они не являются  независимыми. Коэффициент  передачи  и  импульсная  характеристика связаны между собой преобразованием Фурье:

                                           

                                                     

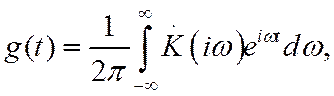
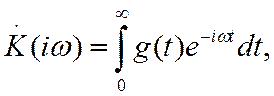
а импульсная характеристика  представляет  собой  производную от переходной характеристики

                                                                                        

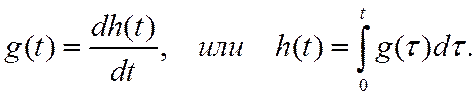
Обсудим теперь вопрос о том, как эти  характеристики  линейной  цепи могут быть найдены. В силу того,  что они представляют  собой  отклик системы на достаточно простые по форме стандартные входные  сигналы, их несложно определить экспериментально.  Действительно,  для того чтобы определить коэффициент передачи 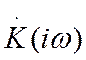, нужно подать  на  вход  системы  гармонический  сигнал   и  измерить параметры выходного сигнала, который в  силу  линейности  системы также будет гармоническим: .  Отношение амплитуд  выходного  и  входного  сигналов  будет  равно   модулю коэффициента передачи на данной частоте, а разность фаз  сигналов  –  фазе  коэффициента  передачи.  Проведя  такие  измерения   в   выбранном диапазоне частот, мы узнаем АЧХ и ФЧХ  системы  в  этом  диапазоне.