Один и тот же по форме сигнал в зависимости от его
длительности может передаваться ФНЧ принципиально по-разному
(разумеется, это утверждение относится также и к другим цепочкам).
Покажем это на примере прямоугольного импульса единичной амплитуды и длительности
![]() (см. рис.4 и выражения (26)). Предположим,
что
(см. рис.4 и выражения (26)). Предположим,
что ![]() , тогда
для частоты
, тогда
для частоты ![]() , на которой располагается первый
нуль огибающей спектра, выполняется соотношение
, на которой располагается первый
нуль огибающей спектра, выполняется соотношение ![]() . В этом случае спектр входного сигнала
располагается, в основном, в той области, где коэффициент передачи близок к
единице (рис. 8,а). Это означает, что прямоугольные
импульсы большой длительности (по сравнению с постоянной времени цепочки)
передаются ФНЧ без существенных искажений.
. В этом случае спектр входного сигнала
располагается, в основном, в той области, где коэффициент передачи близок к
единице (рис. 8,а). Это означает, что прямоугольные
импульсы большой длительности (по сравнению с постоянной времени цепочки)
передаются ФНЧ без существенных искажений.
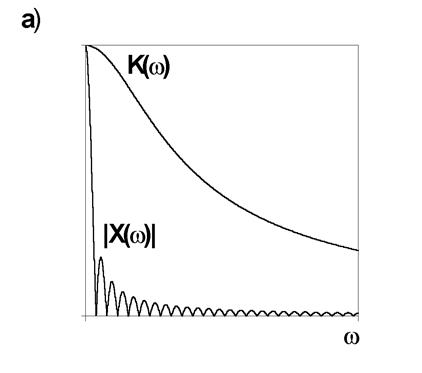
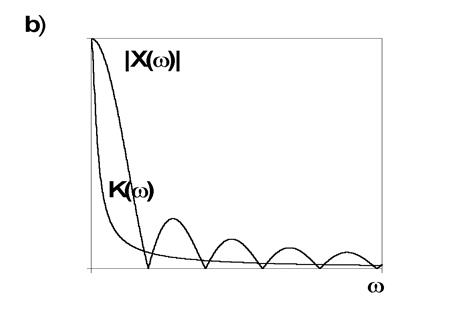
Рис. 8
Если на вход интегрирующей цепочки подается импульс малой
длительности ![]() , то
, то ![]() и
практически во всей области частот, занимаемой спектром, выполняется
соотношение
и
практически во всей области частот, занимаемой спектром, выполняется
соотношение 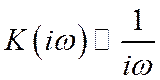 (рис. 8б). Следовательно, такой
входной сигнал данной цепочкой будет приближенно проинтегрирован. Далее мы
подтвердим эти качественные выводы точными расчетами.
(рис. 8б). Следовательно, такой
входной сигнал данной цепочкой будет приближенно проинтегрирован. Далее мы
подтвердим эти качественные выводы точными расчетами.
Приступим теперь к определению переходной и импульсной характеристик интегрирующей цепочки. Напишем для нее уравнение Кирхгофа
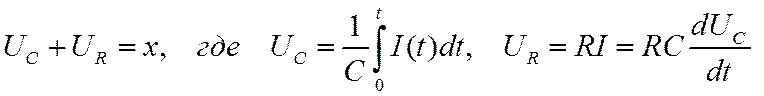
Обозначая ![]() , получим
следующее уравнение, связывающее входной и выходной сигналы:
, получим
следующее уравнение, связывающее входной и выходной сигналы:
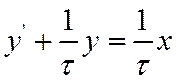
Для
определения переходной характеристики ![]() нужно
подать на вход сигнал в виде функции единичного включения
нужно
подать на вход сигнал в виде функции единичного включения ![]() . Напомним, что в силу принципа причинности
. Напомним, что в силу принципа причинности
![]() при
при ![]() .
При
.
При ![]() значение выходного сигнала
определяется из уравнения
значение выходного сигнала
определяется из уравнения
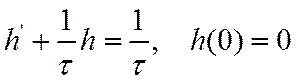
Выходной сигнал при ![]() равен
нулю, так как напряжение на емкости не может измениться скачком, а до этого момента
емкость была не заряжена. Общее решение уравнения (40) имеет вид
равен
нулю, так как напряжение на емкости не может измениться скачком, а до этого момента
емкость была не заряжена. Общее решение уравнения (40) имеет вид
![]()
Константа ![]() находится из начального
условия:
находится из начального
условия: ![]() . Следовательно, переходная
характеристика интегрирующей цепочки описывается следующей функцией:
. Следовательно, переходная
характеристика интегрирующей цепочки описывается следующей функцией:
![]()
с учетом (25) импульсная характеристика при ![]() равна
(рис.9)
равна
(рис.9)
![]()
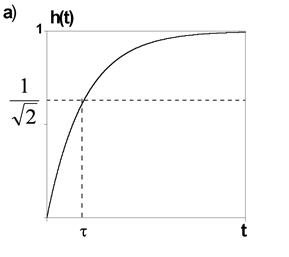 Рис. 9
Рис. 9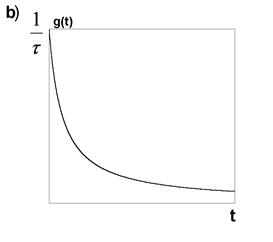
При ![]() значение
значение ![]() достигает уровня 0.63 от своего
максимального значения; это время можно использовать для оценки длительности
"фронта" выходного сигнала. Найденная переходная характеристика
позволяет нам рассчитать искажение прямоугольного импульса фильтром НЧ.
Представим этот сигнал в виде двух функций единичного включения:
достигает уровня 0.63 от своего
максимального значения; это время можно использовать для оценки длительности
"фронта" выходного сигнала. Найденная переходная характеристика
позволяет нам рассчитать искажение прямоугольного импульса фильтром НЧ.
Представим этот сигнал в виде двух функций единичного включения:
![]()
Выходной сигнал в этом случае равен
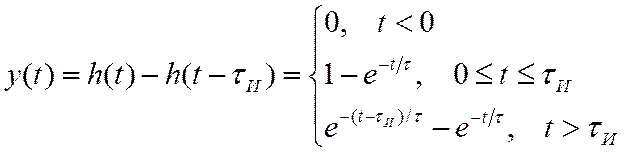
При
![]() длительность переднего и заднего фронтов
много меньше длительности самого сигнала, такой прямоугольный импульс
проходит через ФНЧ без существенных искажений (рис. 10,а).
длительность переднего и заднего фронтов
много меньше длительности самого сигнала, такой прямоугольный импульс
проходит через ФНЧ без существенных искажений (рис. 10,а).
При
![]() заменим входящую в (45) экспоненту двумя
первыми слагаемыми ряда Тейлора. В результате получим:
заменим входящую в (45) экспоненту двумя
первыми слагаемыми ряда Тейлора. В результате получим:
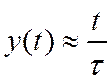
Учитывая,
что в это время ![]() , мы действительно
получили приближенное интегрирование входного сигнала (ср. (46) и (37)) –
см. рис. 10б.
, мы действительно
получили приближенное интегрирование входного сигнала (ср. (46) и (37)) –
см. рис. 10б.
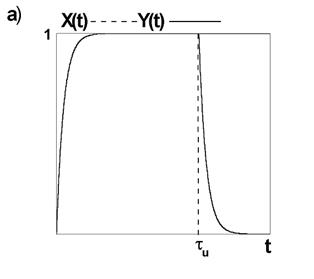
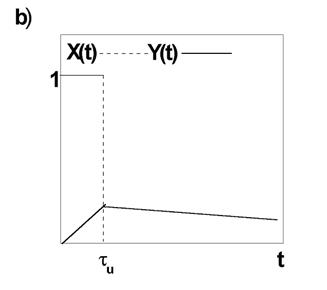
Рис. 10
Выходной сигнал (45) может быть рассчитан также
спектральным методом. Для этого подставим выражения для спектра прямоугольного
импульса (26) и для коэффициента передачи ФНЧ (32), заменив в них ![]() на
на![]() , в выражение (22):
, в выражение (22):
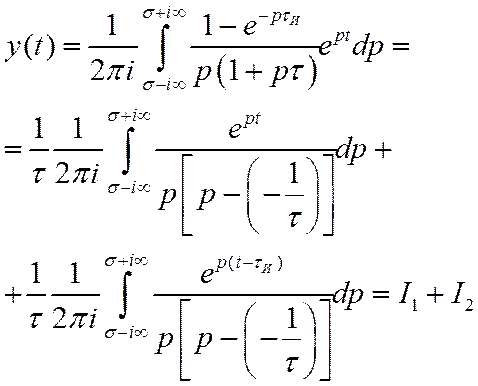
Полюсы
подынтегральных функций в ![]() и
и ![]() расположены одинаково – в точках
расположены одинаково – в точках ![]() и
и ![]() .
Однако для вычисления
.
Однако для вычисления ![]() по лемме Жордана нужно
замыкать контур интегрирования направо при
по лемме Жордана нужно
замыкать контур интегрирования направо при ![]() и
налево при
и
налево при ![]() , а для
, а для![]() – направо при
– направо при ![]() и
налево при
и
налево при ![]() .
.
Вычислив ![]() и
и ![]() , получим:
, получим:
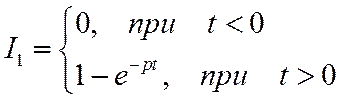
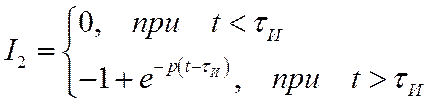
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.