Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 2

Из курса математики известно, что общее решение дифференциального уравнения (4) (выходной сигнал) представляет собой сумму общего решения  однородного уравнения 

                                           

с ненулевыми начальными условиями   и  частного решения    неоднородного уравнения (4) с нулевыми начальными условиями. 

Другими словами, выходной сигнал можно представить в виде суммы реакций системы на ненулевые начальные условия и на входной сигнал. Ненулевые начальные условия реализуются тогда, когда к моменту включения входного сигнала  в реактивных элементах схемы (индуктивностях и емкостях) была запасена энергия. Такие случаи   встречаются  достаточно  редко,  и мы в дальнейшем будем  предполагать начальные условия нулевыми, поэтому  и, следовательно, , т. е. источником  выходного сигнала является только входное воздействие.

Основные методы анализа линейных систем.

Приступим теперь к решению задачи о  том,  как  в  общем  виде определить  выходной  сигнал    при  произвольном   входном воздействии  для произвольной линейной системы.  Решить ее можно, опираясь на принцип  суперпозиции.  Он  заключается в следующем: если на вход линейной системы воздействуют одновременно несколько сигналов  , то выходной сигнал будет представлять собой сумму сигналов  , где  есть  реакция системы на входное воздействие  при отсутствии  остальных.

Справедливость этого принципа достаточно очевидна. Действительно, так как параметры линейной системы не зависят от приложенных к ее элементам  напряжений  и  протекающих через них токов, то на прохождение через нее сигнала  остальные входные воздействия никакого влияния оказать не могут. То есть каждое входное воздействие распространяется через линейную систему независимо от присутствия остальных.

Задачу о прохождении произвольного сигнала через линейную систему мы сможем  решить в общем виде, если нам удастся представить входное воздействие в виде суммы   "стандартных" сигналов и определить реакцию системы на это стандартное воздействие. Поясним это подробно на конкретных примерах.

Возьмем сначала в качестве таких стандартных сигналов ступенчатую функцию  ,  включаемую в момент времени (рис. 2,а).  

                                                             

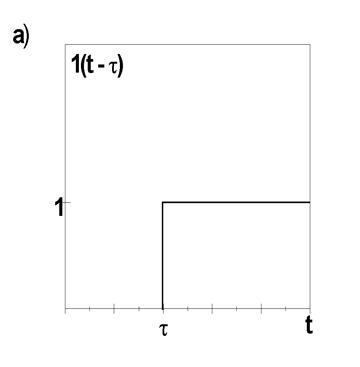
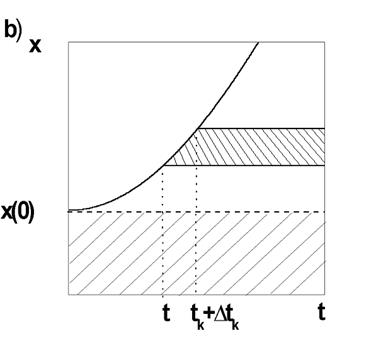
Рис. 2

Любой входной сигнал можно представить в виде набора сигналов такой формы  (рис. 2,б). Очевидно, что нижний заштрихованный сигнал равен  .  Верхний  заштрихованный сигнал имеет амплитуду  и поступает на вход системы при  ; следовательно, он равен .

Таким образом, входной сигнал приближенно описывается следующей суммой:

                             

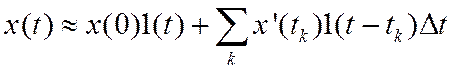
Предположим, что нам известна реакция системы на входное воздействие в виде  функции единичного включения . Обозначим такую реакцию и  назовем функциюпереходной характеристикой линейной системы. О том, как ее можно найти и каковы ее свойства, будет сказано ниже.

Зная переходную характеристику  системы,  можно определить выходной сигнал. Используя представление  в  виде  (6)  и учитывая принцип суперпозиции, получим

                           

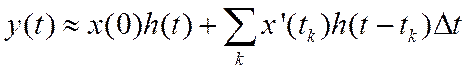
При стремлении  нужно заменить сумму соответствующим интегралом, и мы получим точное выражение для выходного сигнала

                              

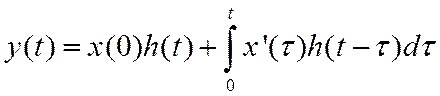
Данное выражение, называемое интегралом Дюамеля, дает нам решение поставленной задачи.

В качестве другого стандартного входного воздействия выберем сигнал прямоугольной формы длительности , площадь которого равна 1, т. е. амплитуды   (рис.3а).  Обозначим  его  . Реакцию линейной системы на такое воздействие обозначим .

    

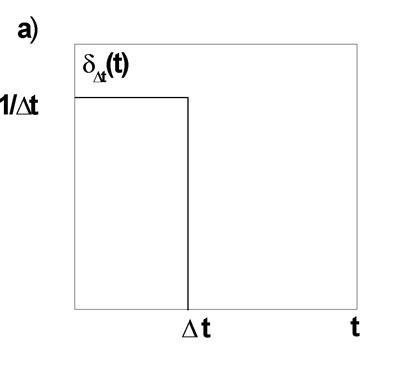
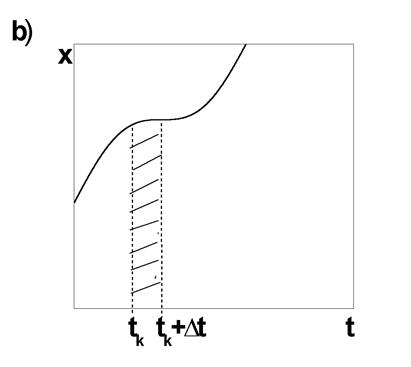
Рис.3

Заштрихованная часть входного сигнала, представленного на рис. 3б, может  быть  записана  так: , а сам входной сигнал

                                             

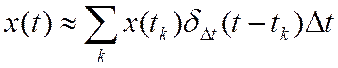
Следовательно, приближенное выражение для выходного сигнала будет иметь вид

                                           

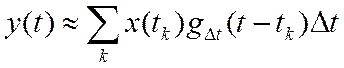
При стремлении  функция  перейдет в обычную -функцию . Получающийся при этом выходной сигнал обозначим  и назовем импульсной характеристикой системы.  Тогда выражение для выходного сигнала  будет представлять собой свертку  входного сигнала и импульсной характеристики системы: