Автоматизированные измерения и моделирование свойств линейных систем: Учебно-методическое пособие, страница 9

sawtooth — генерация периодического пилообразного сигнала,

square — генерация периодической последовательности прямоугольных импульсов,

tripuls — генерация одиночного треугольного импульса.

Для построения АЧХ и ФЧХ фильтра можно использовать команду freqs(b, a)  в рабочем окне MATLAB. Параметры этой команды – векторы коэффициентов полиномов, соответственно числителя и знаменателя коэффициента передачи.

Для примера рассмотрим симметричную цепочку Вина (рис. 15). Комплексный коэффициент передачи (57) можно записать как:

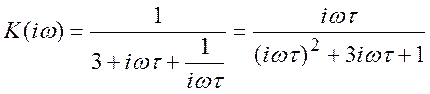                                    ,  (75)

Тогда вектор числителя будет b = [τ  0] (сомножитель τ при первой степени iω и нет слагаемого с нулевой степенью iω) и аналогично вектор знаменателя a = [ τ²  3τ  1]. Для определенности выберем τ = 1, тогда ω₀ тоже будет равно 1 и листинг команд в Matlab будет:

a=[1 3 1];

b=[1 0];

freqs(b,a);

Результатом выполнения этих команд являются АЧХ и ФЧХ цепочки Вина (рис. 19).

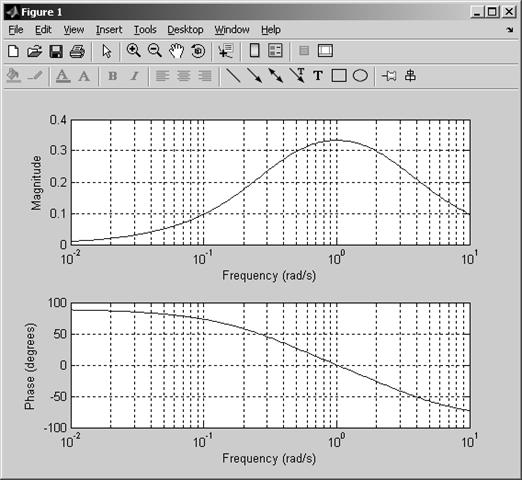
Рис. 19

Рассмотрим теперь некоторые возможности Simulink, использующиеся при решении задач линейной аналоговой фильтрации. При моделировании в Simulink реализуется принцип визуального программирования, в соответствии с которым пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты.

Любая модель, создаваемая в рамках данной лабораторной работы, содержит блоки-источники сигналов, блоки-регистраторы сигналов, и блоки, описывающие саму линейную систему. Для построения Simulink-модели (S-модели), необходимо выполнить расстановку блоков на схеме, задать их параметры, соединить блоки и установить параметры расчета модели в целом. В качестве источников могут выступать блоки, представленные на рис.20.

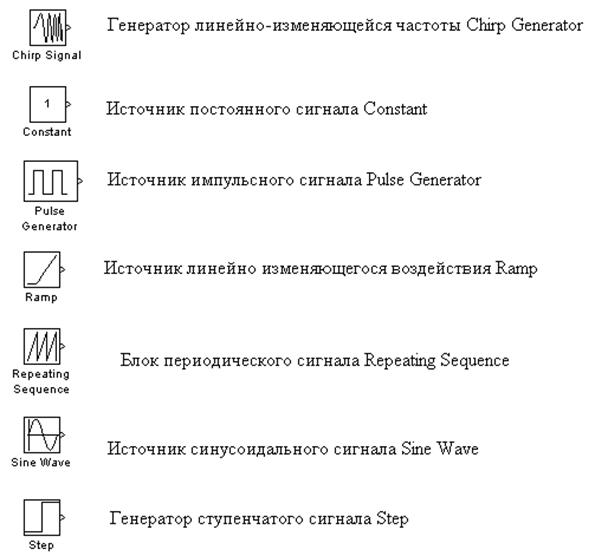
Рис. 20

В качестве регистраторов можно использовать следующие блоки (рис. 21):

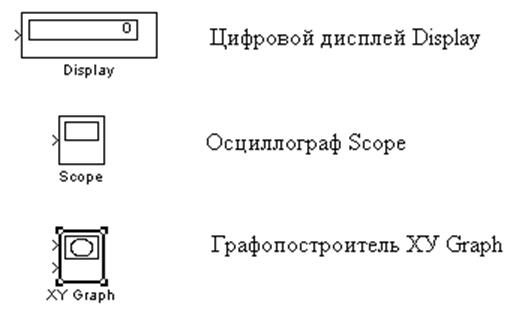
Рис. 21

Осциллограф и графопостроитель позволяют наблюдать за изменениями сигналов в процессе моделирования. Осциллограф строит сигнал как функцию времени, а графопостроитель строит график одного сигнала как функцию другого. Эти блоки позволяют изменять масштабы отображаемых графиков. В параметрах блока осциллограф можно выбрать число входов осциллографа и максимальное количество отображаемых расчетных точек графика. При превышении числа отображаемых расчетных точек графика начальная часть графика обрезается. В этом случае можно убрать флажок параметра Limit data points to last, тогда Simulink автоматически увеличит значение этого параметра для отображения всех расчетных точек.

Саму линейную систему в Simulink можно моделировать двумя различными способами. Первый из них предполагает использование блока Transfer Fcn. В этом случае система описывается коэффициентом передачи (28) представленном в виде:

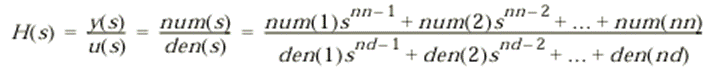   ,                                                                (76)

где nn и nd – порядок числителя и знаменателя передаточной функции, а
num и den – вектора коэффициентов числителя и знаменателя соответственно, аналогичные векторам b и a команды Matlab freqs(b,a).

В качестве примера рассмотрим дифференцирующую RC-цепочку. Делая замену iω=s в выражении (50) для коэффициента передачи этой цепочки, получим:

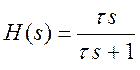                                                                                (77)

Simulink-модель будет выглядеть следующим образом (рис. 22):

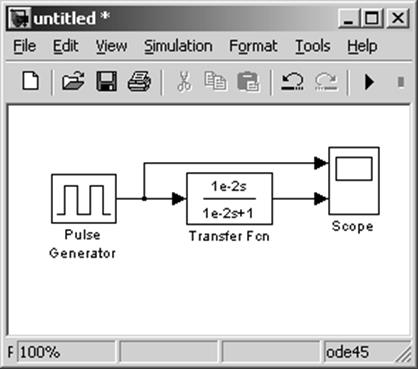
Рис. 22

В модели последовательность прямоугольных импульсов, вырабатываемая генератором прямоугольных импульсов PulseGenerator, проходит через дифференцирующую RC-цепочку. Цепочка моделируется блоком Transfer Fcn. Результат выводится на экран двухлучевого осциллографа Scope.

На рис. 23 показан экран осциллографа. Верхний график изображает исходную последовательность прямоугольных импульсов, нижний – сигнал, прошедший через цепочку.

Временной и частотный анализ линейных систем удобно проводить с помощью специального инструмента Simulink LTI-Viewer, который входит в состав пакета прикладных программ Control System Toolbox и предназначен для анализа линейных стационарных систем. С помощью данного инструмента можно легко построить частотные характеристики исследуемой системы, получить ее отклики на единичные ступенчатое и импульсное воздействия и т.д.