Линейные аналоговые системы. Пространство состояний. Дифференциальное уравнение

Линейные аналоговые системы.

Импульсная характеристика h(t).

Это реакция системы на поданную на вход дельта-функцию.

s_вх(t) = _-∞∫^∞ s_вх(t’)δ(t-t’)dt’

s_вых(t) = _-∞∫^∞ s_вх(t’)h(t-t’)dt’

Переходная характеристика g(t).

Это реакция системы на поданную на вход функцию единичного скачка.

h(t)=dg(t)/dt

g(t)=_-∞∫^t s_вх(t’)h(t-t’)dt’

Комплексный коэффициент передачи K(w).

S_вых(iw) = S_вх(iw)K(iw)

K(iw) - преобразование Фурье от импульсной характеристики.

K(iw) = _-∞∫^∞ h(t)e^-iwtdt

Модуль K(iw) – АЧХ

Фаза K(iw) – ФЧХ

Функция передачи H(s).

Линейная система с сосредоточенными параметрами может быть представлена в виде ДУ. Если применить в ДУ преобразование Лапласа, то получиться выражение для функции передачи.

H(s) = (b_ms^m+b_m-1s^m-1 + … + b₁s + b₀)/( a_nsⁿ+a_n-1s^n-1 + … + a₁s + a₀)

m ≤ n

K(iw) получается подстановкой s = iw

Разложив H(s) на множители:

H(s) = k(s-z_m) (s-z_m-1)/((s-p_n) (s-p_m-1))

k=b_m/a_n– коэффициент усиления

z_i – нули функции передачи

p_i – полюсы функции передачи

Разложив H(s) на сумму:

H(s) = r_n/(s-p_n) + r_n-1/(s-p_n-1) +…+ r₁/(s-p₁)+C₀

p_i – полюсы функции передачи

r_i – вычеты

при наличии кратных полюсов, каждый m-кратный полюс p_i дает m слагаемых вида

r_i1/(s-p_i) + r_i2/(s-p_i)² + r_i3/(s-p_i)³+…+ r_im/(s-p_i)^m

Представление H(s) в виде суммы простых дробей позволяет вычислить h(t)

Слагаемое ФП  r_i/(s-p_i) соответствует слагаемому ИХ r_iexp(p_it), t≥0

Для кратных полюсов:

r_i1exp(p_it) + r_i2 t exp(p_it) + …+ r_im t^m-1 exp(p_it) /(m-1)!

Пространство состояний

Еще один способ описания ЛС. Состояние цепи описывается вектором s(t), а собственные колебания цепи и ее реакции на входной сигнал x(t) характеризуются следующим образом:

s’(t) = A s(t)+B x(t)

y(t) = C s(t)+Dx(t)

Если

s(t) – вектор столбец размерностью N

x(t), y(t) - скаляры

A – матрица NxN

B– столбец Nx1

C – строка 1xN

D – скаляр

Если

x(t), y(t) – вектора, то размерности параметров меняются.

Описанием цепи является набор параметров A, B, C, D

Если применить преобразование Лапласа, то

H(s) = D – C(A - sI)^-1B

I – Единичная матрица NxN

Дифференциальное уравнение

Для линейной системы с сосредоточенными параметрами R,L,C дифференциальное уравнение можно записать в следующем виде.

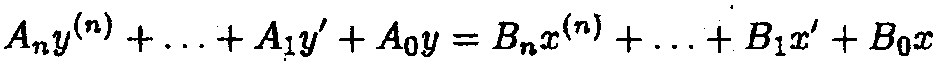
где x(t) – входной сигнал

Общее решение уравнения y(t) (выходной сигнал) представляет собой сумму общего решения однородного уравнения y₁(t) с ненулевыми начальными условиями и частного решения неоднородного уравнения y₂(t) с нулевыми начальными условиями. Ненулевые начальные условия реализуются очень редко (когда при t=0 в реактивных элементах была запасена энергия), поэтому будем предполагать начальные условия нулевыми y₁(t) = 0. Следовательно, y(t) = y₂(t), т.е., источником выходного сигнала является только входное взаимодействие.

Коэффициент передачи может быть рассчитан теоретически.

Положим 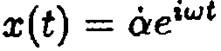, тогда выходной сигнал будем искать в виде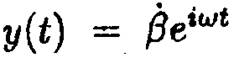. Подставляя В ДУ получим

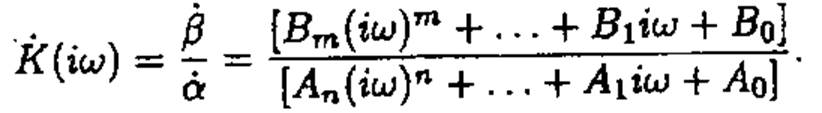
Описанный способ нахождения коэффициента передачи не всегда удобен, т.к. требует предварительного написания ДУ, что достаточно трудоемко для систем высокого порядка.

Для расчета коэффициента передачи может быть использован символический метод. Его суть в замене в схеме реактивных элементов их комплексными сопротивлениями.

Пусть ток через индуктивность

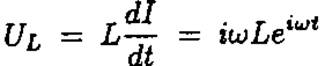
Тогда комплексное сопротивление индуктивности

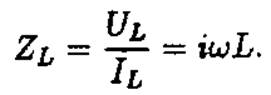
Для емкости

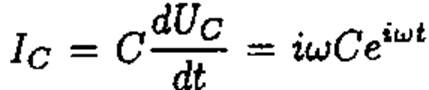
Тогда комплексное сопротивление емкости

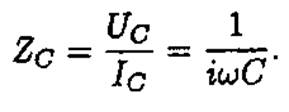
Например, для схемы

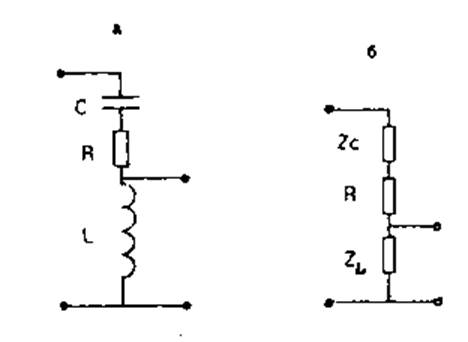
Коэффициент передачи будет имеет вид:

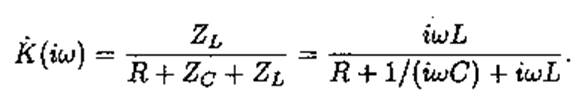
Зная K(iw) можно найти переходную и импульсную характеристику.

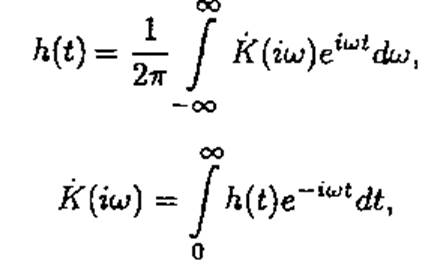
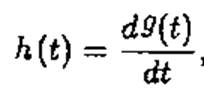
Рассмотрим конкретный пример:

Пример 1

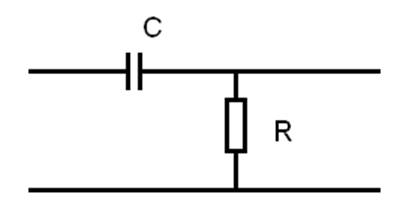
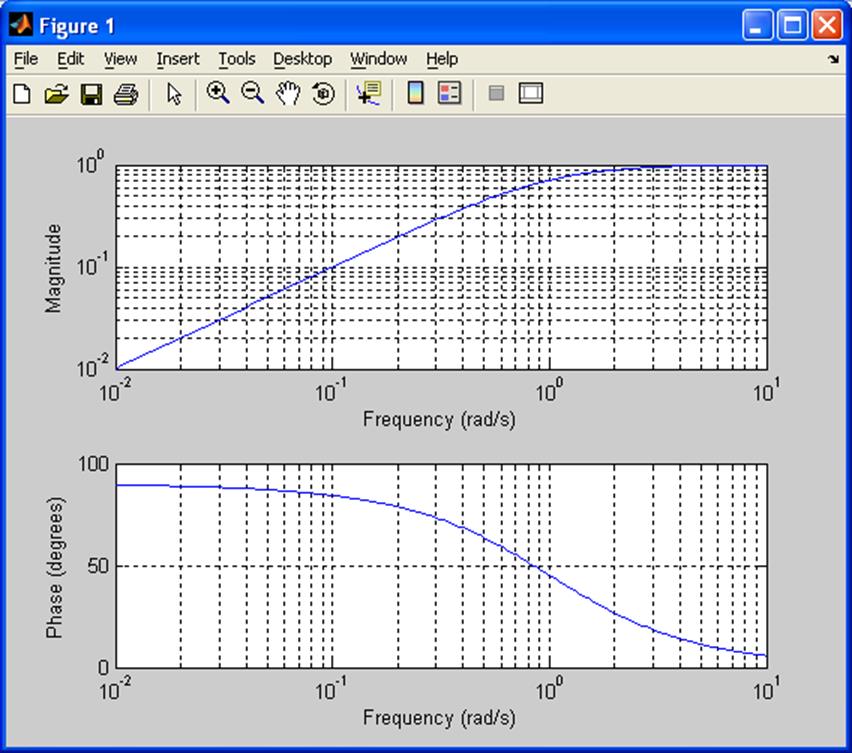
Данная цепочка является фильтром высоких частот с коэффициентом передачи:

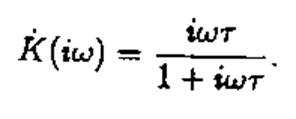
АЧХ и ФЧХ описываются следующими функциями:

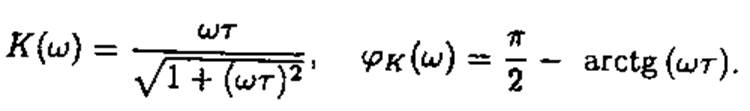
t=RC – постоянная времени.

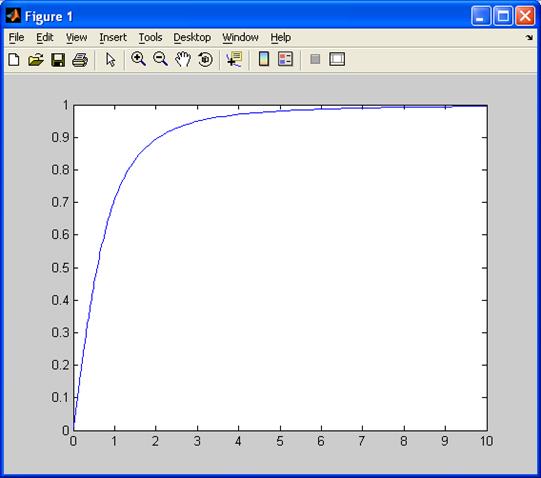
 Импульсная и переходная характеристика имеют вид:

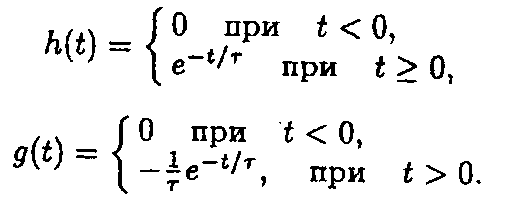
Пусть через данную цепочку проходит прямоугольный импульс.

s(t) = 1, при  0≤t≤t

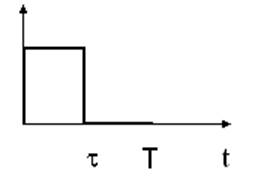
S(iw) = t sin(wt/2)exp(-iwt/2)/(wt/2)

t = p

T=2p

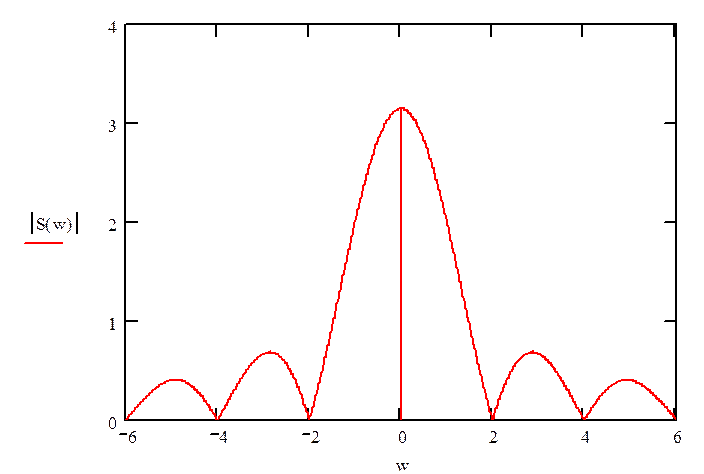
Построим спектр прямоугольного импульса в Matlab.

Команда FFT - Одномерное дискретное прямое и обратное преобразования Фурье

Синтаксис:

Y = fft(X)            X = ifft(Y)

Y = fft(X, n)        X = ifft(Y, n)

Описание:

Дискретные прямое и обратное преобразования Фурье для одномерного массива x длины N определяются следующим образом:

 

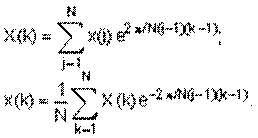
Функция Y = fft(X) вычисляет для массива данных X дискретное преобразование Фурье, используя FFT-алгоритм быстрого Фурье-преобразования. Если массив X двумерный, вычисляется дискретное преобразование каждого столбца.

Функция Y = fft(X, n) вычисляет n-точечное дискретное преобразование Фурье. Если length(X) < n, то недостающие строки массива X заполняются нулями; если length(X) > n, то лишние строки удаляются.

Функция X = ifft(Y) вычисляет обратное преобразование Фурье для массива Y.

Функция X = ifft(Y, n) вычисляет n-точечное обратное преобразование Фурье для массива Y.

Зная спектр сигнала и коэффициент передачи цепочки, можно определить спектр выходного сигнала. Для гармоники надо умножить на соответствующие коэффициенты.

Пусть для простоты RC = 1, тогда K(iw) = iw/(1+iw)

Рассмотрим программу в MATLAB

clear

clc

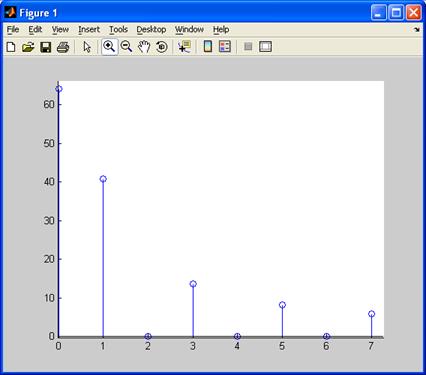
Создаем входной сигнал( прямоугольный импульс длительностью t = p

и периодом T=2p)

tau=3.142

for i=1:64

s(i)=1;

end

for i=65:128

s(i)=0;

end

for i=1:128

t(i)=2*tau*i/128;

end   

figure

plot(t,s);

grid

Строим преобразование Фурье

s2=fft(s);

s3=abs(s2);

w=[0:1:127]

figure

stem(w,s3);

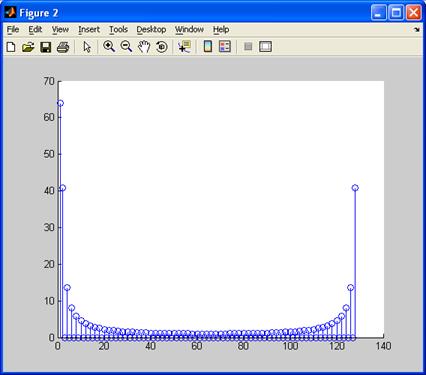
Умножаем спектр входного сигнала на коэффициент передачи

(причем сначала умножаем гармоники до N/2 - й ,а далее отражаем гармоники симметрично относительно N/2 – й с комплексным сопряжением)

rc=1

s2_v(1)=s2(1)

for i=1:65

    s2_v(i)=s2(i)*1i*w(i)*rc/(1+1i*w(i)*rc);

end

p=0;

for i=66:128

p=p+1;

    s2_v(i)=conj(s2_v(65-p));

end

s3_v=abs(s2_v);

figure

stem(w,s3_v);

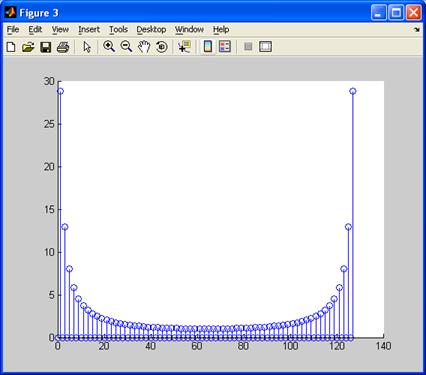
Строим обратное преобразование Фурье

s_v=ifft(s2_v);

figure

plot(t,s_v);

grid

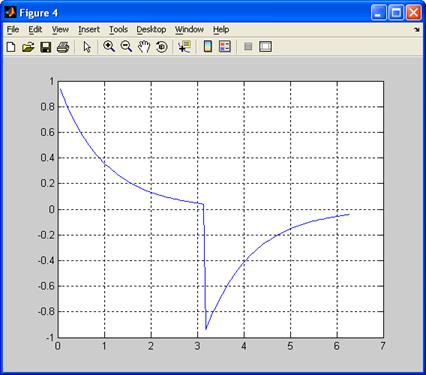
Команда freqs