Описание ЛДС в Z-области
Передаточная функция.
![]() - основная характеристика ЛДС в Z-области.
- основная характеристика ЛДС в Z-области.
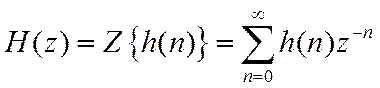
Справедливо обратное преобразование
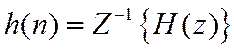
Было рассмотрено 2 способа описания ЛДС во временной области: 1) с помощью формулы свертки, 2) с помощью разностного уравнения.
Применим к обеим частям соответствующих равенств z-преобразование.
Начнем с формулы свертки.
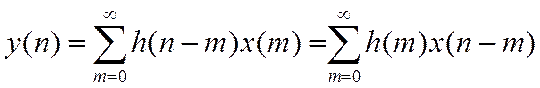
Из свойств Z-преобразования
![]()
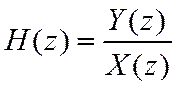
Из (5) можно получить (1)
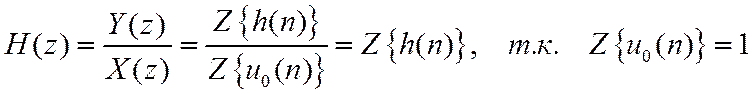
Из РУ
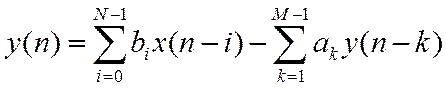
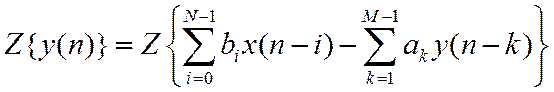
Из линейности и теоремы запаздывания
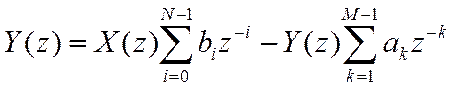
Запись ПФ в общем виде
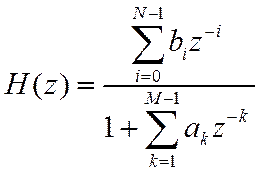
Т.о., ПФ – дробно-рациональная функция от ![]() с вещественными коэффициентами, степень
полинома числителя равна N-1, знаменателя M-1.
с вещественными коэффициентами, степень
полинома числителя равна N-1, знаменателя M-1.
Порядок ПФ – максимальное из чисел N-1
и M-1. Далее будем считать ![]()
Для определения нулей и полюсов ПФ числитель и знаменатель
(10) предварительно умножают на ![]() .
.
Взаимосвязь передаточной функции и РУ
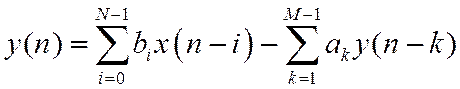
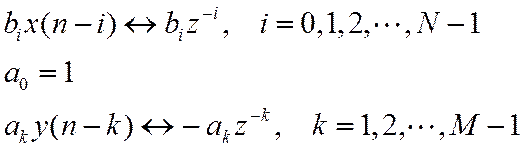
Пример.
Задана ПФ
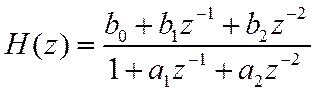
Найти РУ
![]()
Разновидности представления ПФ
Различные представления ПФ обусловлены либо возможностью их различного математического представления, либо различным типом ЛДС: КИХ и БИХ.
БИХ-системы
1. Представление ПФ в виде произведения с разложением числителя и знаменателя на простейшие множители первой степени
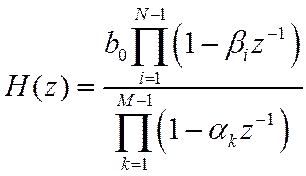
![]() - нули и полюсы ПФ, в общем
случае – комплексно сопряженные числа.
- нули и полюсы ПФ, в общем
случае – комплексно сопряженные числа.
2. Представление ПФ в виде произведения с разложением числителя и знаменателя на множители второй степени
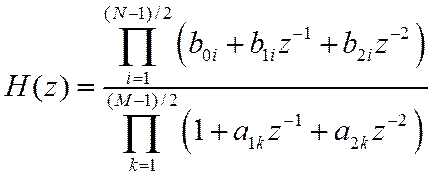
![]() - вещественные коэффициенты, (N-1), (M-1) – четные числа.
- вещественные коэффициенты, (N-1), (M-1) – четные числа.
Если (N-1) или (M-1)
– нечетные числа, то верхний индекс произведения равен N/2
или M/2. При этом ![]() или
или ![]() , т.е. один нуль или полюс будет
вещественным.
, т.е. один нуль или полюс будет
вещественным.
(12) получается из (11) перемножением сомножителей с комплексно-сопряженными корнями. Покажем это на примере
![]()
Тогда
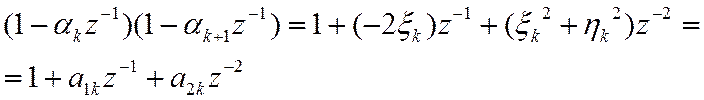
3. Представление ПФ в виде суммы простых дробей первой
степени ![]()
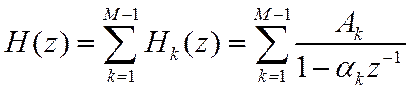
В общем случае полюсы – комплексно-сопряженные (так
же, как и коэффициенты ![]() ).
).
Если N>M, то разложение будет иметь вид (С.198)
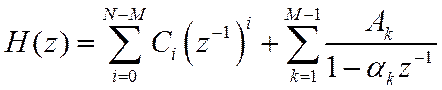
Если полюс ![]() имеет кратность m, то в разложении на простейшие ему будет соответствовать
сумма
имеет кратность m, то в разложении на простейшие ему будет соответствовать
сумма
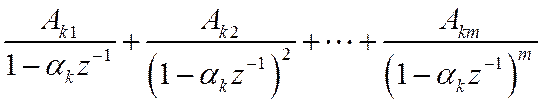
4. Представление ПФ в виде суммы дробей второй
степени ![]()
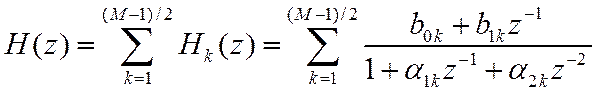
(14) получается из (12) путем суммирования слагаемых с комплексно-сопряженными полюсами.
Дополнительно для БИХ-систем выделяют ПФ полюсного типа
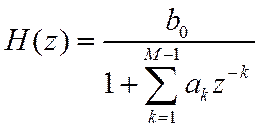
Текущий выходной отсчет зависит от текущего входного и (M-1) выходных отсчетов.
В этом случае ПФ можно представить, разложив знаменатель на простейшие множители первого порядка
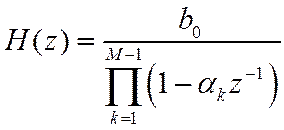
или второго порядка
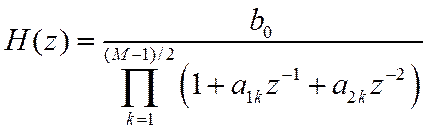
А также в виде суммы простых дробей первого (13) или второго (14) порядка.
КИХ-системы
Нерекурсивные ЛДС описываются ПФ вида
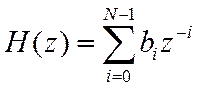
(18) может быть представлены в виде разложения на простейшие сомножители первого порядка
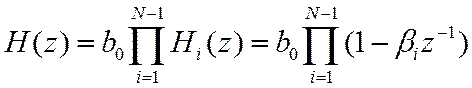
или второго порядка
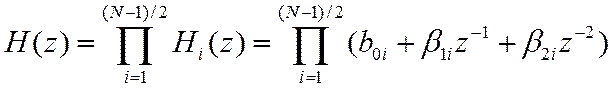
ПФ и ИХ базовых звеньев первого и второго порядка
Для базового звена первого порядка
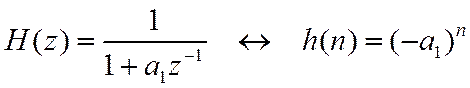
Для базового звена второго порядка
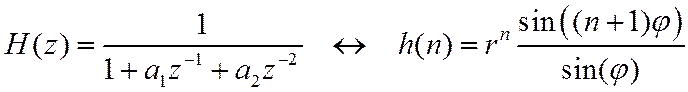
где ![]() и
и![]() -
модуль и аргумент комплексно-сопряженных полюсов
-
модуль и аргумент комплексно-сопряженных полюсов
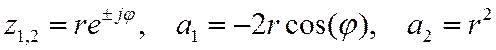
Для записи ИХ не базового звена нужно воспользоваться свойствами линейности и пропорциональности Z-преобразования, а также теоремой о запаздывании.
Для звена первого порядка
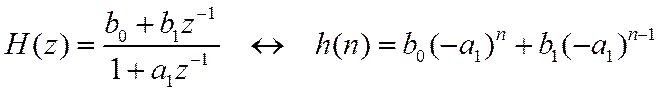
С учетом начальных условий
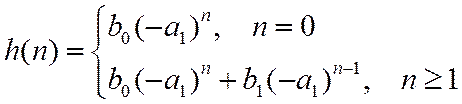
Для звена второго порядка
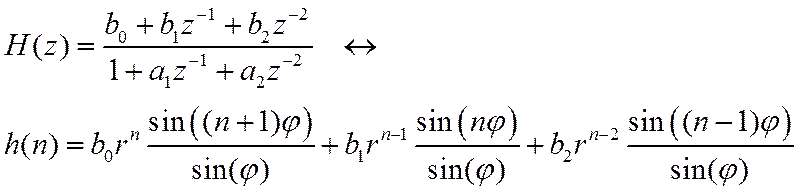
С учетом нулевых начальных условий
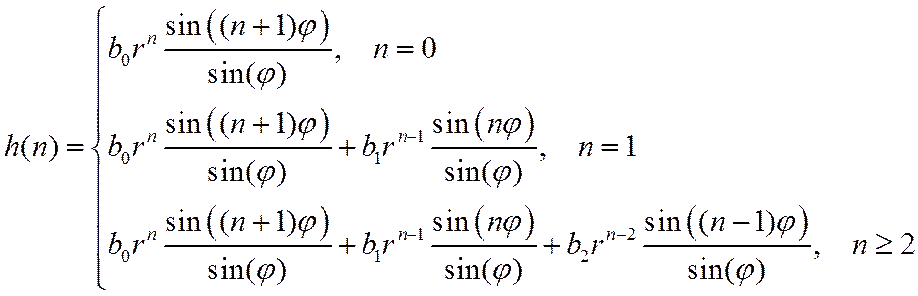
Оценка устойчивости ЛДС по ПФ
Был получен критерий устойчивости по ИХ
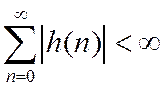
Записав ПФ в виде суммы простых дробей первой степени (13), получим выражение для ИХ
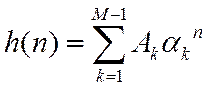
Тогда
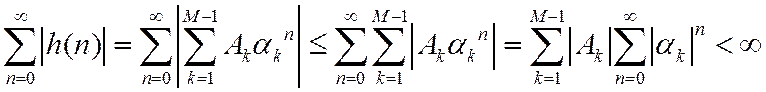
выполняется, если
![]()
Т.е., ДЛС устойчива, если все полюсы ее ПФ располагаются внутри единичной окружности на Z-плоскости.
Карты нулей и полюсов звеньев первого и второго порядка.
Звено первого порядка
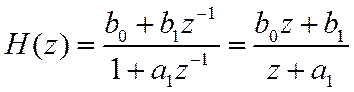
имеет вещественные ноль и полюс
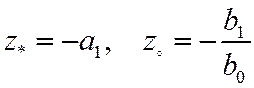
Звено второго порядка
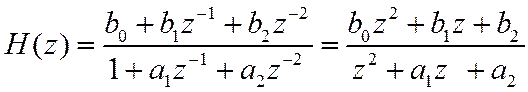
имеет, как было показано в примере Z-преобразования, комплексно-сопряженные полюсы
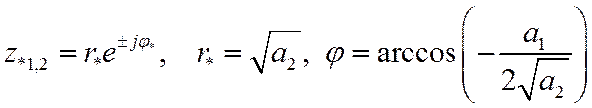
Выражение для нулей
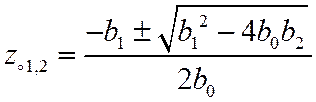
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.