Описание ЛДС в частотной области
Была введена ПФ как Z-преобразование от ИХ
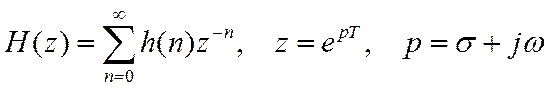
Покажем, что в случае ![]() ПФ
равна отношению гармонического дискретного сигнала на выходе к гармоническому
сигналу на входе. Т.е. сужение ПФ на единичную окружность дает нам ЧХ
дискретной системы.
ПФ
равна отношению гармонического дискретного сигнала на выходе к гармоническому
сигналу на входе. Т.е. сужение ПФ на единичную окружность дает нам ЧХ
дискретной системы.
![]()
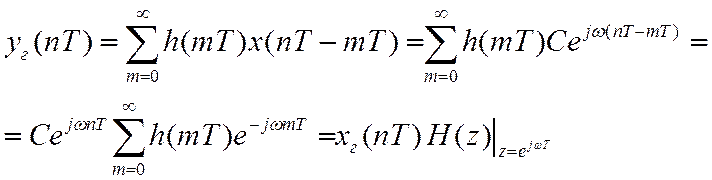
Частотная характеристика ЛДС определяется как
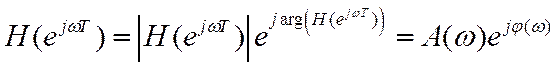
Значит гармонический дискретный сигнал, прошедший через ЛДС, есть гармонический сигнал с той же частотой. Измениться может только его амплитуда и фаза.
![]()
Свойства ЧХ ЛДС.
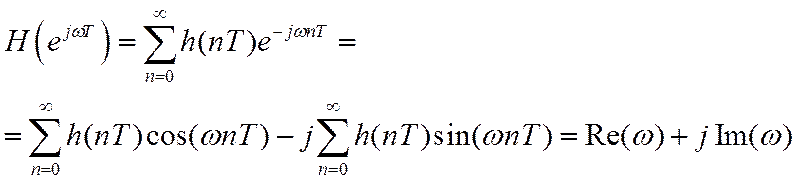
![]()
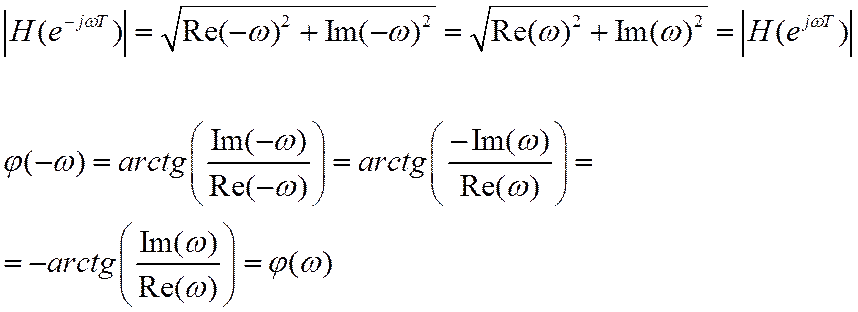
Учитывая общее выражение для ПФ
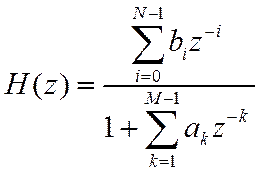
получим общее выражение для ЧХ
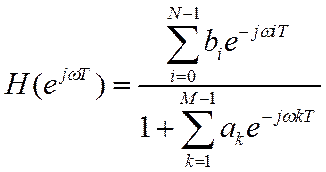
Т.к. ПФ есть дробно-рациональная функция, то согласно основной теореме алгебры она всегда может быть представлена в виде
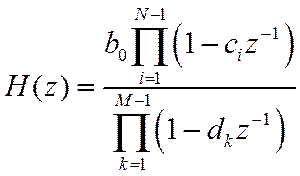
Т.о., ЧХ с точностью до константы полностью определяется своими нулями и полюсами.
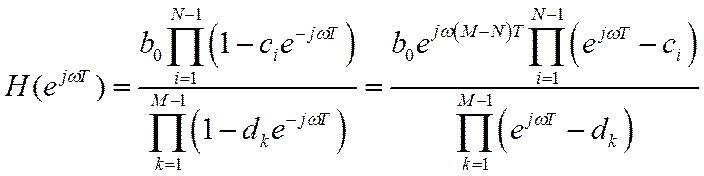
АЧХ и ФЧХ ЛДС имеют вид
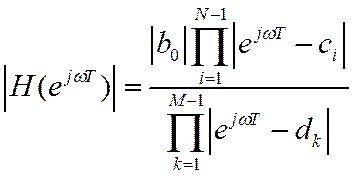
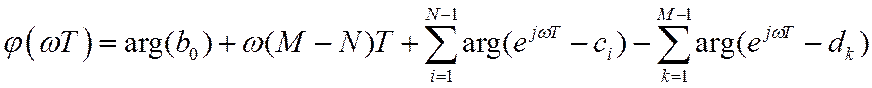
Пример. (Вас.78)
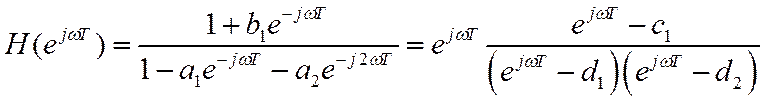
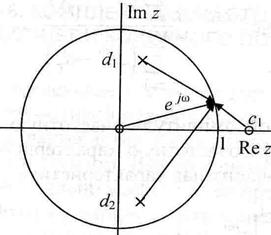
Всепропускающие цепи.
Рассмотрим устойчивую ЛДС с одним нулем и полюсом, определяемые выражениями
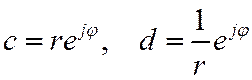
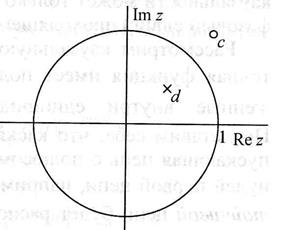
Ее ЧХ
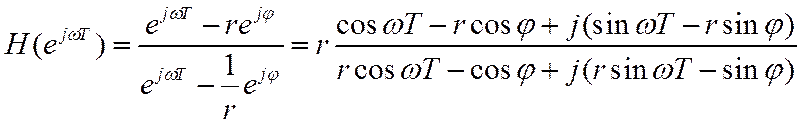
![]()
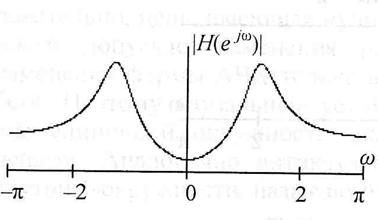
АЧХ и ФЧХ этой цепи приведены на рис.
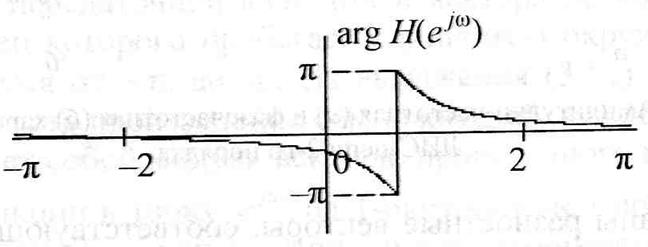
ЛДС с линейной ФЧХ.
Линейность ФЧХ обеспечивает сохранение формы сигнала, если его спектр укладывается в полосу пропускания фильтра. Рассмотрим цепь с четным числом отсчетов импульсной характеристики, которая четно-симметрична относительно своей середины (КИХ-система).
![]()
Запишем ЧХ в виде
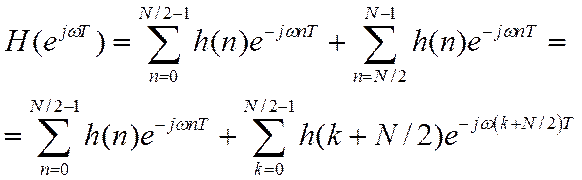
Рассматривая слагаемые во второй сумме в обратном порядке
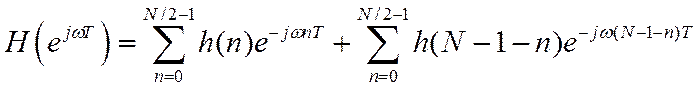
С учетом условия симметрии отсчетов
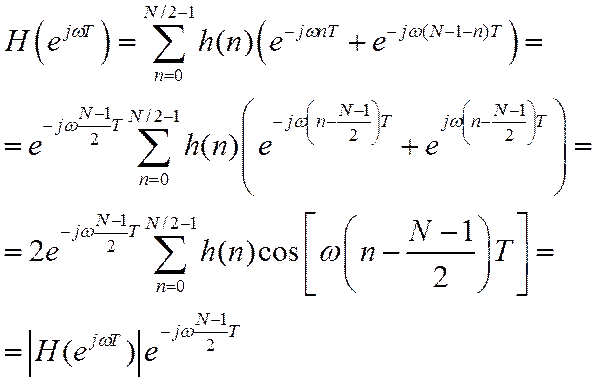
Наклон ФЧХ определяется номером среднего отсчета.
Каузальные БИХ-цепи с линейной АЧХ не существуют. Фильтры Бесселя имеют приближенно линейную ФЧХ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.