Синтез цифровых фильтров. Синтез БИХ-фильтров. Синтез КИХ-фильтров

Синтез ЦФ

Задача синтеза ЦФ как задача аппроксимации. Требования к фильтру формулируются чаще всего в форме желаемой АЧХ, реже – ФЧХ. Т.е. ставится задача аппроксимации ПФ. Для КИХ фильтров ПФ – полином, для БИХ – дробно-рациональная функция. При синтезе д. б. выполнены требования физической реализуемости и устойчивости (для КИХ).

Этапы проектирования ЦФ:

1. определение требований к фильтру;
2. решение задачи аппроксимации характеристик фильтра при помощи реализуемой КИХ или БИХ цепи;
3. реализация структурной схемы с учетом эффектов квантования и ошибок округления.

Методы синтеза КИХ и БИХ фильтров различны, т.к. различны методы аппроксимации желаемых характеристик полиномами и дробно-рациональными функциями.

Синтез БИХ фильтров основан на преобразовании аналоговых фильтров-прототипов в цифровые фильтры. Сначала рассчитывается фильтр прототип выбранного типа (Баттерворта, Чебышева I или II рода, эллиптический и т.д.) с заданными характеристиками. Затем синтезируется цифровой фильтр методом инвариантности ИХ или методом билинейного Z-преобразования. Существует также возможность синтеза ЦФ произвольного типа по цифровому прототипу ФНЧ.

Синтез КИХ фильтров чаще всего осуществляют следующими методами. Методом взвешивания, основанным на аппроксимации ПФ конечной суммой ряда Фурье с введением весовых (оконных) последовательностей. Методом частотной выборки, основанным на интерполяции ПФ полиномом Лагранжа. Методом быстрой свертки, основанном на алгоритме быстрого преобразования Фурье.

Синтез БИХ фильтров

Методы синтеза БИХ-фильтров основаны на аналого-цифровой трансформации.

Аналоговые фильтры-прототипы. Рассматриваются только ФНЧ, т. к. остальные типы можно получить путем частотных преобразований.

1. Фильтры Баттерворта.

Максимальная гладкость АЧХ. Требование равенства нулю  производных знаменателя квадрата АЧХ в точке w=0, кроме старшей производной.

                                                                     

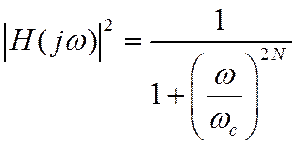
Следовательно, для ПФ

                                                        

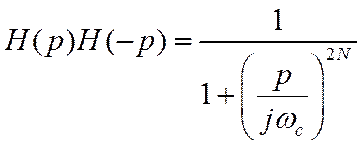
Полюсы квадрата ПФ определяются из уравнения

                                                                                                   

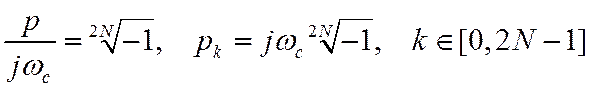
Корней 2N, и они расположены равномерно на окружности радиуса . При трансформации аналогового фильтра Бесселя в цифровой методом билинейного z-преобразования эта окружность переходит в окружность z-плоскости, но полюсы расположены на ней неравномерно.

 

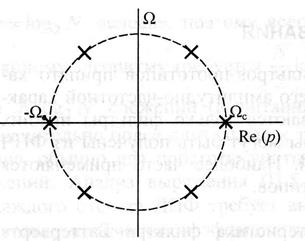
На рис. Представлено распределение полюсов для фильтра Баттерворта 3-го порядка.

Чтобы фильтр был устойчивым, нужно, чтобы полюсы функции H(p) лежали в левой полуплоскости, а функции H(-p) – в правой. При любом N АЧХ монотонна, а ее значение на  равно .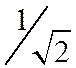

2. Фильтры Чебышеева.

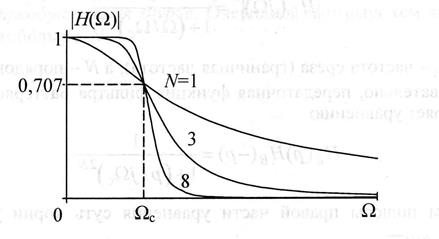
Аппроксимация желаемой АЧХ, основанная на полиномах Чебышева, обеспечивает более быстрый спад АЧХ в переходной полосе за счет осцилляций АЧХ в полосе пропускания (фильтры 1-го рода), или в полосе подавления (фильтры второго рода). Полином Чебышева порядка n.

                                              

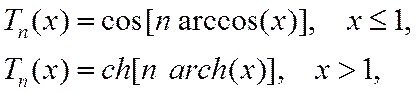
Справедливы рекуррентные соотношения

                                                                                             

Полином Чебышева при  осциллирует между значениями [-1,1], а при x>1 монотонно возрастает. Поэтому функция

                                                         

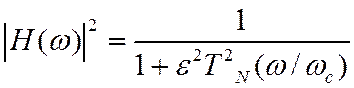
при , то есть в полосе пропускания осциллирует между значениями 1 и , а за пределами этой полосы монотонно убывают.

Передаточная функция фильтра Чебышева удовлетворяет уравнению

                                            

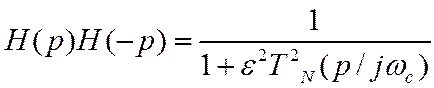
Полюсы правой части лежат на эллипсе, заключенном между двумя окружностями радиусов

                                                                               

      

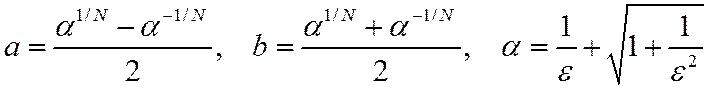
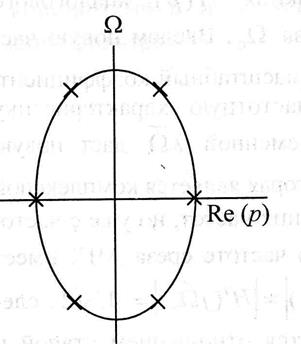
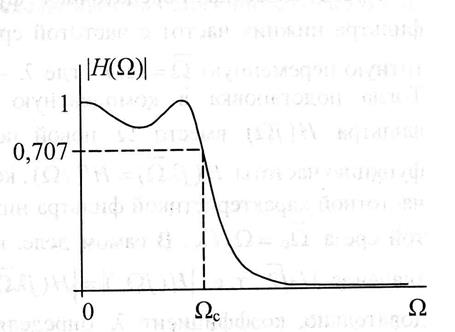
Фильтры Чебышева второго рода

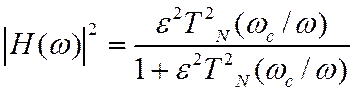
3. Эллиптические фильтры Золотарева-Кауэра.

Эллиптические фильтры обеспечивают еще большую крутизну АЧХ в переходной области за счет осцилляций, как в полосе пропускания, так и в полосе задерживания. Для них

                                                        

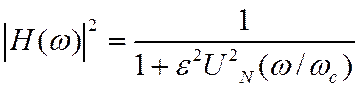
Преобразование частоты позволяет получить фильтр заданного типа из ФНЧ.

1. ФНЧ – ФНЧ:

                                                                        

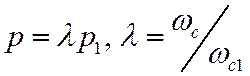
2. ФНЧ – ФВЧ:

                                                                      

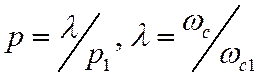
3. ФНЧ – ППФ:

                                                                                             

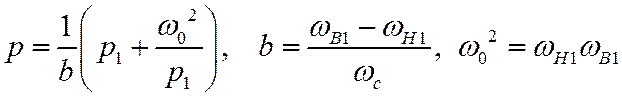
4. ФНЧ – РФ: