Синтез цифровых фильтров. Синтез БИХ-фильтров. Синтез КИХ-фильтров, страница 4

Очевидно, что , поэтому точки  являются корнями полинома . Следовательно,

                                                                            

                                               

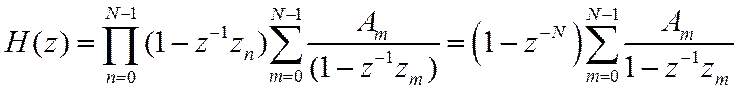
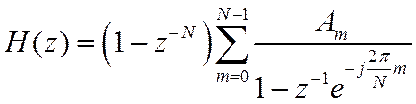
Структура фильтра будет наиболее простой, если в большинстве узлов интерполяции значение ПФ =0, т.е. для узкополосных фильтров.

Быстрое преобразование Фурье

Алгоритмы используют симметрию ДПФ для группирования данных с целью уменьшения числа операций. Рассматривается алгоритм с прореживанием по времени. (Вас. 372).

Рассмотрим ДПФ последовательности x(n) по основанию .

                                     

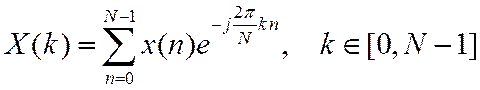
Введем обозначение 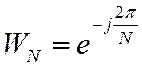, с учетом которого

                                                                                    

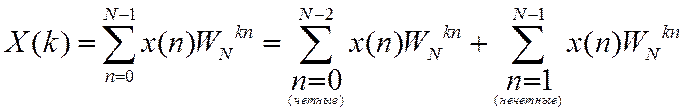
Введем новый индекс  для четных n и  для нечетных n. Тогда

                                                                                                           

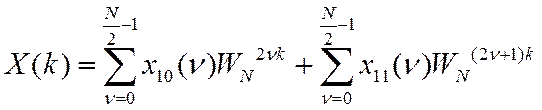
где .

Рассмотрим первую сумму.

                                      

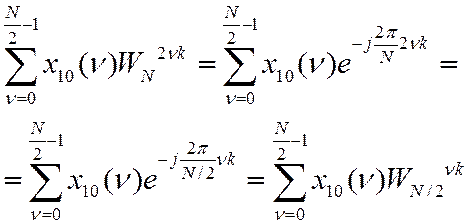
Это есть N/2 точечное ДПФ от подпоследовательности с четными номерами.

Аналогично

                                                                                                       

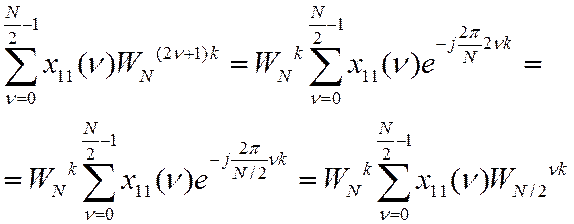
Таким образом, ДПФ последовательности x(n) может быть выражено через ДПФ двух последовательностей вдвое меньшей длины:

                                                                                                     

Получено выражение для вычисления половины отсчетов ДПФ исходной последовательности.

Учтем, что коэффициенты ДПФ образуют периодическую последовательность с периодом, равным количеству отсчетов преобразуемой последовательности. Поэтому   и  имеют период N/2. Поэтому вторая половина отсчетов определится следующим образом

                                                                                      

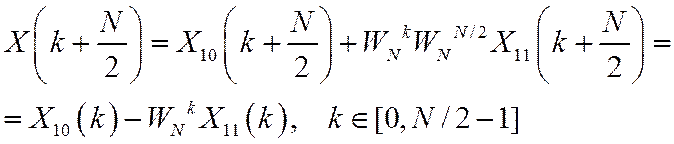
Итак, ДПФ последовательности x(n) может быть выражено через ДПФ четной и нечетной подпоследовательности  при всех значениях k.

Пример. 8-точечное ДПФ. Может быть сведено к двум 4-точечным, которые в свою очередь сводятся к четырем 2-точечным.

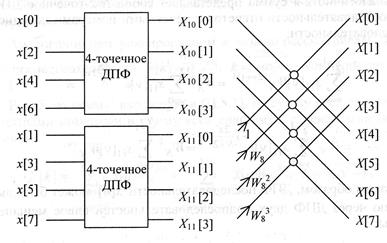
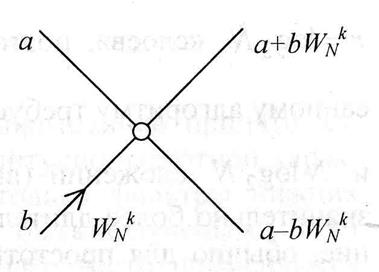
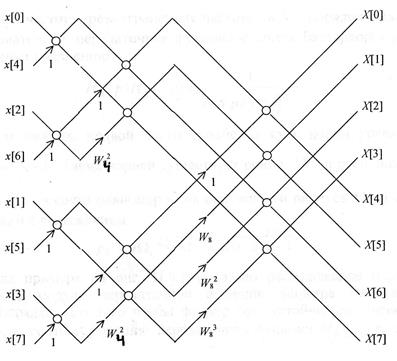
На правый слой схемы требуется примерно N/2 умножений. Также и для других слоев. Если число точек , то число слоев равно . Поэтому число операций умножения, необходимых для вычисления БПФ равно

                                                                                       

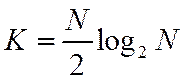
вместо  умножений при непосредственном вычислении ДПФ. Следовательно получается выигрыш в

                                                                                                     

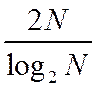
раз. Например, для  N=1024 число умножений уменьшается в 200 раз.

3. Метод КИХ-фильтрации на основе быстрой свертки. (Вас.146)

Воздействие ЛДС на входную последовательность полностью описывается сверткой ИХ с входной последовательностью. В некоторых случаях удобно заменить свертку перемножением z-образов. Это дает преимущества благодаря существованию эффективных алгоритмов ДПФ – алгоритмов БПФ.

Практически z-преобразование может быть выполнено только в конечном числе точек, поэтому выполнение свертки косвенным путем – через перемножение z-образов возможно только для последовательностей конечной длины. Поэтому такой метод фильтрации применим только для КИХ-фильтров.

Метод КИХ-фильтрации последовательностей путем поточечного умножения их ДПФ-спектров на ПФ цепи на основе БПФ называется методом быстрой свертки.

Пусть x(n) и h(n) – числовые последовательности длины N. Их свертка

                                                                  

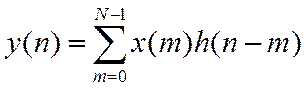
ДПФ этой последовательности

                                                                                  

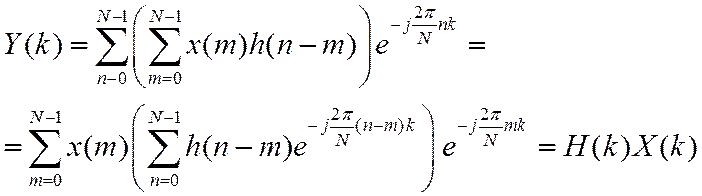
Т.о., поточечное перемножение дискретных спектров соответствует свертке последовательностей одинаковой длины. Если длина последовательностей  x(n) или h(n) меньше требуемой для БПФ, то их дополняют нулями. Это не изменяет результат свертки, но позволяет поточечно перемножать их спектры.

При реализации данного метода для фильтрации входных последовательностей большой длины применяют метод сегментации. Пусть ИХ имеет конечную длину М, а входная последовательность – бесконечна. Представим ВП в виде суммы не перекрывающихся сегментов длины L

                                                                                        

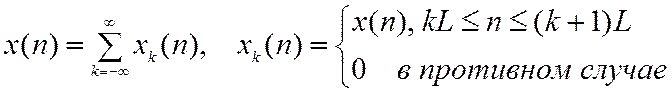
В силу линейности свертки

                                             

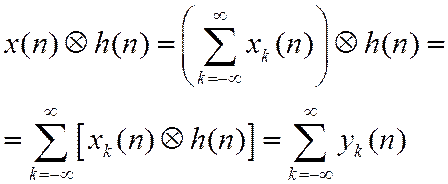
Т.о., результат каждой частичной свертки имеет длину L+M-1, а следуют секции с относительным сдвигом L.