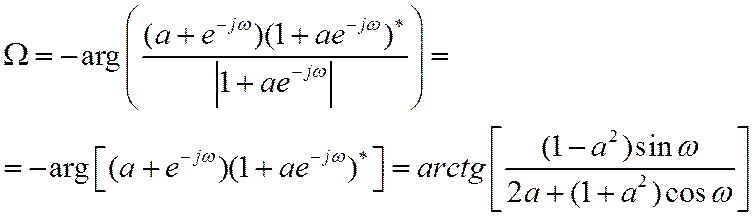
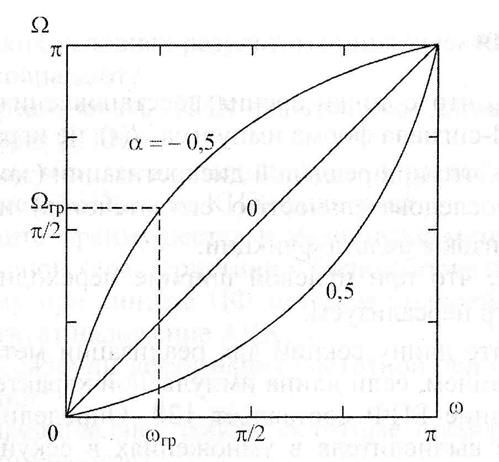
Связь частот
Параметр a определяется, исходя из значений частот среза
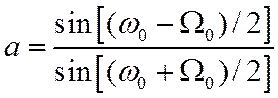
Преобразование ФНЧ в ФВЧ
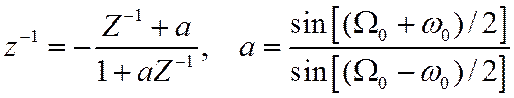
Преобразование ФНЧ в ППФ
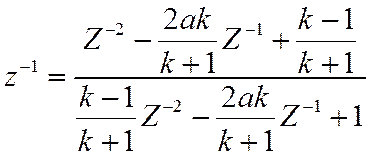
с параметрами
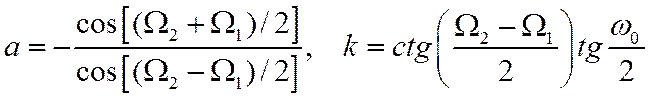
Преобразование ФНЧ в РФ
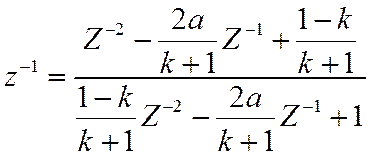
с параметрами
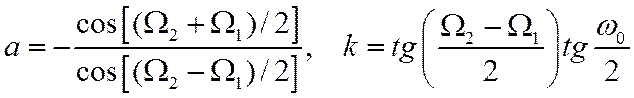
Синтез КИХ-фильтров.
1. Метод взвешивания (метод оконных функций).
ПФ нерекурсивного фильтра представляет собой полином. Для ![]()
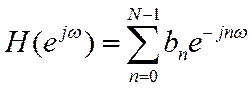
В качестве критерия близости ЧХ ЦФ к желаемой ЧХ ![]() возьмем среднеквадратическую ошибку
аппроксимации
возьмем среднеквадратическую ошибку
аппроксимации
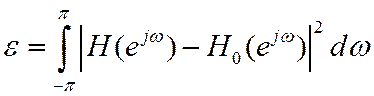
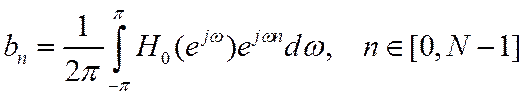
Коэффициенты (3), стоящие в (1) являются отсчетами ИХ фильтра. Из-за усечения ряда (1) на ЧХ фильтра появляются гиббсовские осцилляции. Поэтому кроме усечения ряда Фурье, применяют умножение отсчетов ИХ на весовую последовательность (оконную функцию).
Эффект Гиббса. (Вас.44)
Идеальный ФНЧ
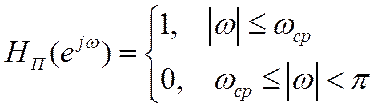
Его ИХ (коэффициенты РФ)
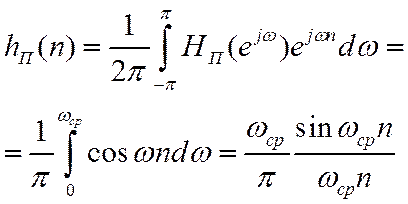
Нет абсолютной сходимости ИХ, поэтому фильтр неустойчив и, следовательно, физически нереализуем.
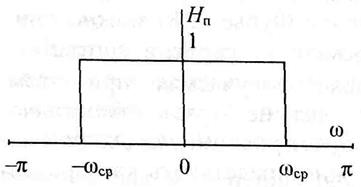
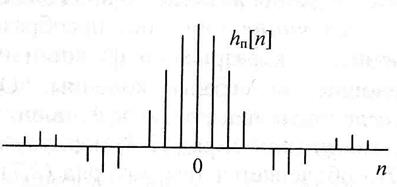
После усечения ИХ
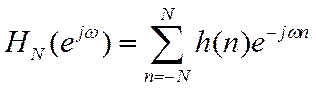
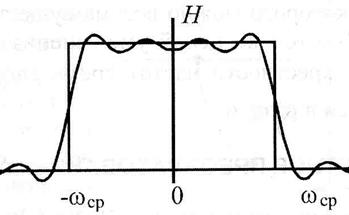
Для уменьшения осцилляций усеченную ИХ умножают на дополнительную весовую последовательность («окно») конечной длины. Подбором окна можно существенно уменьшить осцилляции ИХ, но только за счет уменьшения крутизны вблизи частоты среза.
1. Прямоугольное окно.
![]()
2. Окно Бартлетта (треугольное)
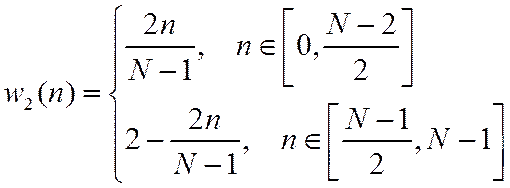
3. Окно Хэнна (Ганна)
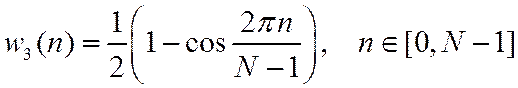
4. Окно Хэмминга
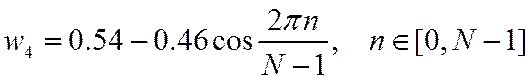
5. Окно Блэкмана
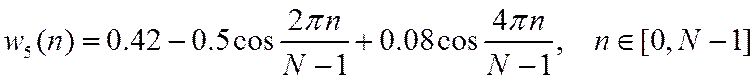
6. Окно Кайзера
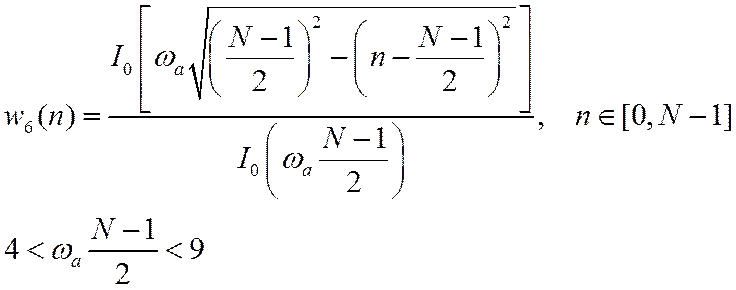
Другой способ борьбы с осцилляциями АЧХ – введение переходной полосы, где задается закон непрерывного изменения АЧХ, например, линейный, или отрезок синуса. Тогда величина осцилляций уменьшается с увеличением порядка фильтра.
Синтез КИХ-фильтров на основе численной оптимизации. Подбором коэффициентов КИХ-фильтра минимизируется взвешенная среднеквадратичная ошибка
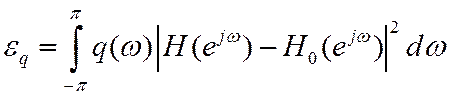
или максимальная взвешенная погрешность
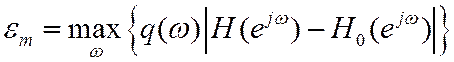
Весовая функция позволяет управлять значимостью ошибки в различных частотных диапазонах.
2. Метод частотной выборки.
Метод основан на построении ПФ, которая совпадает с желаемой ПФ в заданных точках на ед. окружности z-плоскости. Это означает, что в этих точках (узлах интерполяции) совпадут частотные характеристики указанных функций.
Интерполяционный полином Лагранжа (Вас. 270).
Пусть на z-плоскости
заданы N несовпадающих точек ![]() , в которых известны значения ПФ
, в которых известны значения ПФ ![]() . Можно построить полином, который
принимает в этих точках заданные значения. Рассмотрим полином
. Можно построить полином, который
принимает в этих точках заданные значения. Рассмотрим полином
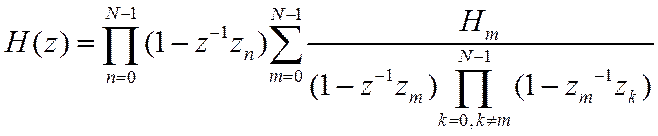
Он полностью определяется значениями функции ![]() и положением узлов интерполяции
и положением узлов интерполяции ![]() . Перепишем это выражение следующим
образом:
. Перепишем это выражение следующим
образом:
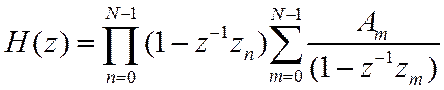
где
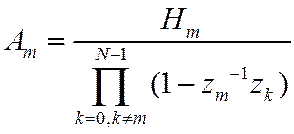
Вычислим ![]() , учтем, что в сумме
(16) можно оставить только одно слагаемое
, учтем, что в сумме
(16) можно оставить только одно слагаемое
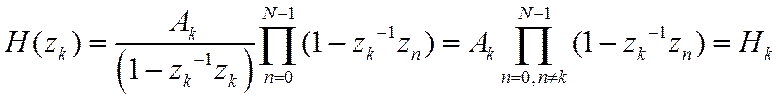
Разместим узлы интерполяции равномерно на единичной окружности
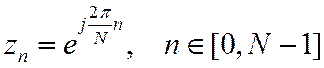
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.