Синтез цифровых фильтров. Синтез БИХ-фильтров. Синтез КИХ-фильтров, страница 2

                                                                                    

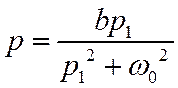
Методы синтеза БИХ-фильтров.

1. Метод инвариантности ИХ.

Связь комплексных переменных p и z.

                                                                      

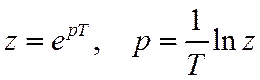
ПФ аналогового фильтра с сосредоточенными параметрами есть дробно-рационльная функция от р. Она может быть представлена суммой дробей

                                                                        

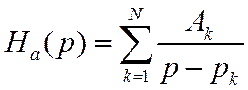
Ввиду линейности преобразования Лапласа ИХ есть сумма экспонент

                                                                                                             

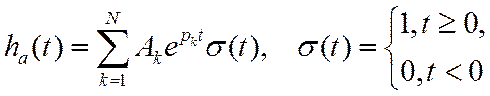
Чтобы ИХ затухала, все полюсы должны располагаться в левой полуплоскости (р).

Метод инвариантности ИХ основан на дискретизации временной функции .

                                                                        

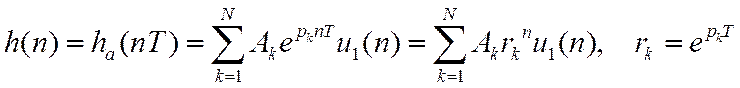
Т.о., реализуемому аналоговому фильтру соответствует реализуемый цифровой фильтр, т.к. полюса лежат внутри единичной окружности

                                                                      

Зная полюсы ЦФ можно написать его ПФ

                                                                         

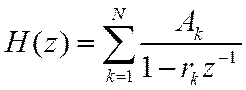
Т.к. ИХ цифрового фильтра получена дискретицацией ИХ аналогового фильтра, то их ПФ связаны соотношением

                                        

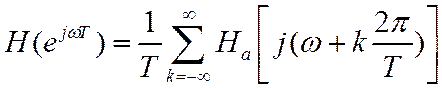
и ПФ аналогового фильтра не ограничена по частоте, то всегда происходит наложение «хвостов» сдвинутых копий аналоговых ПФ. Поэтому этот метод годится в основном для синтеза НЧ фильтров.

2. Метод билинейного z-преобразования.

Способ преобразования аналогового фильтра в цифровой в передаточную функцию  выражения 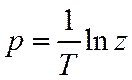 невозможен, так как получающаяся при этом ПФ не будет дробно-рациональной относительно , и, следовательно, не будет физически реализуемой. Воспользуемся разложением логарифма в ряд Тейлора

                                                                                        

или

                                                                                

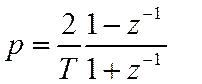
Такая замена оставляет ПФ дробно-рациональной.

Выясним, в какое множество z-плоскости переходит мнимая ось р-плоскости.

                                                              

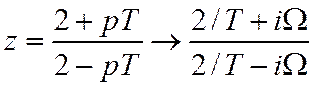
Числитель и знаменатель этой дроби – комплексно-сопряженные, поэтому модуль =1. Поэтому мнимая ось переходит в единичную окружность. В каких пределах изменяется «аналоговая» частота  и «цифровая» частота ? Заменим

                                                 

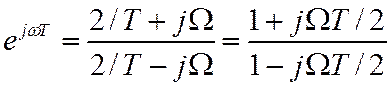
Тогда

                                                                                                               

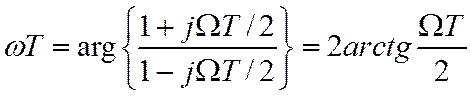
Следовательно,

                                             

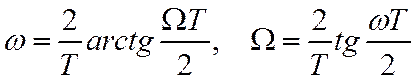
Соотношение частотных осей .

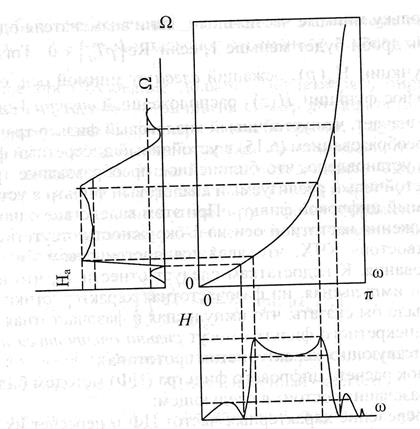
Устойчивость при трансформации. Нужно, чтобы левая полуплоскость P отображалась внутрь единичной окружности Z.

                                                                                                              

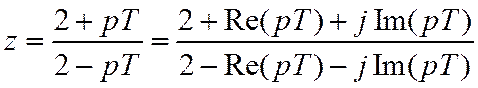
Т.к. мнимые части одинаковы, то |z|<1 если Re(pT)<0. Следовательно, устойчивый аналоговый фильтр трансформируется в устойчивый цифровой.

3. Метод частотного преобразования ЦФ.

Если имеется ЦФ НЧ, то фильтр другого типа можно построить на его основе, используя специально разработанные частотные преобразования.

Пусть есть фильтр с ПФ ,  ПФ желаемого фильтра обозначим . Частотные преобразования переводят плоскость z . После преобразования фильтр должен остаться реализуемым и устойчивым. Этими свойствами обладает преобразование Константинидиса

                                                                                                            

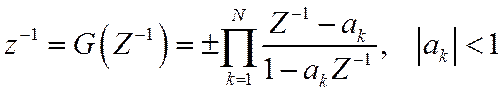
Частотное преобразование в общем виде записывается следующим образом

                                                                  

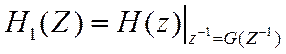
 Преобразование ФНЧ в ФНЧ с другими параметрами.

                                                                                                       

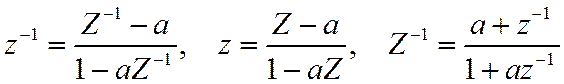
 Рассмотрим преобразование единичной окружности . В этом случае

                                                                                                       

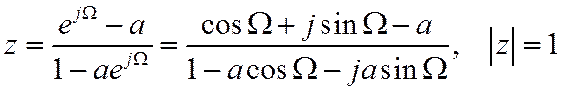
Следовательно, точка z при таком отображении также находится на единичной окружности.

При Z=a значение z=0. Следовательно, внутренняя область 1 круга также находится внутри 1 круга. Т.о., данное преобразование удовлетворяет всем необходимым требованиям.

Преобразование частотной оси. Произведя подстановки , получим

                                                                                

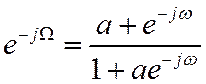
Откуда