Описание ЛДС во временной области. Импульсная характеристика. Формула свертки

Описание ЛДС во временной области

Системой обработки сигналов называют объект, осуществляющий заданное преобразование входного сигнала в выходной.

Будем подразумевать, что система имеет один вход и один выход.

Преобразование «вход-выход» запишем в операторном виде

                                                                                                   

Система линейна, если выполняется

а). свойство аддитивности (принцип суперпозиции)

                                                              

б). свойство однородности

                                                                                       

Система стационарна, если задержка воздействия на приводит только к задержке отклика на то же самое время  (это не относится к аналоговым системам с распределенными параметрами).

Система называется дискретной, если воздействие и отклик – дискретные сигналы (последовательности отсчетов) и .

Будем рассматривать стационарные линейные дискретные системы.

Импульсная характеристика. Формула свертки.

Подобно ЛАС, ЛДС полностью описывается своей импульсной характеристикой.

ИХ   – реакция ЛДС на единичный цифровой импульс  при нулевых НУ. Обозначив начальный момент времени , нулевые НУ можно записать

                                                                 

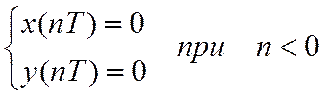
что соответствует принципу причинности.

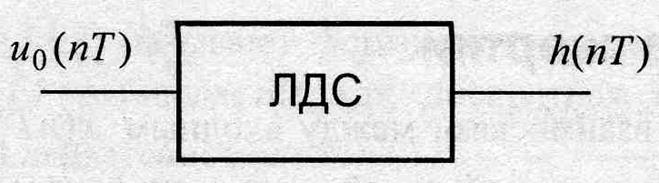
Рис. 4.2.

Кроме ИХ при писании ЛС иногда используют переходную характеристику – реакцию на единичное включение .

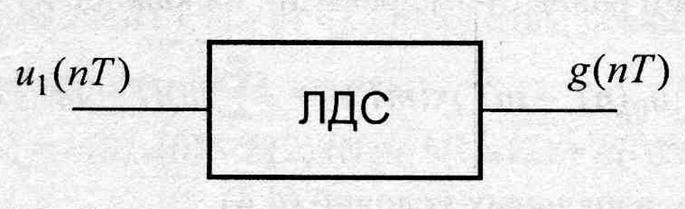
Рис. 4.3.

Во временной области ЛДС описывается формулой свертки (если используется ИХ) или разностным уравнением (если используются параметры системы). Рассмотрим первый способ.

По определению .

Из стационарности .

Из однородности .

Из аддитивности .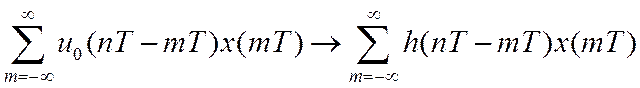

Из-за нулевых НУ .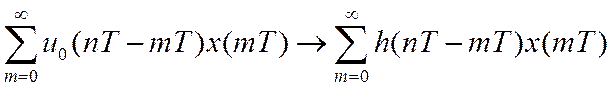

Учитывая, что ,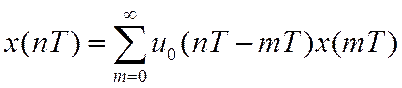

получим  искомую формулу свертки

                                             .        

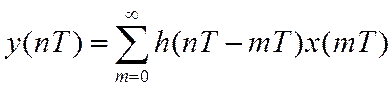Выполнив замену переменных, можно получить другую запись свертки

                                                     

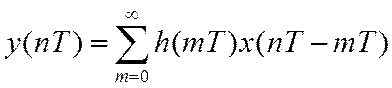
Для нормированного времени

                                                    ,               

                                                                    

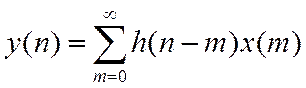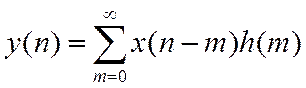
В выходном сигнале  будут следующие слагаемые, вызванные первым элементом входной последовательности :

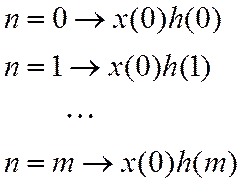
Входной отсчет  даст слагаемые

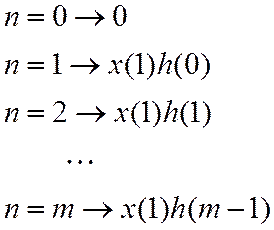
Т.о., будут сформированы отсчеты выходного сигнала

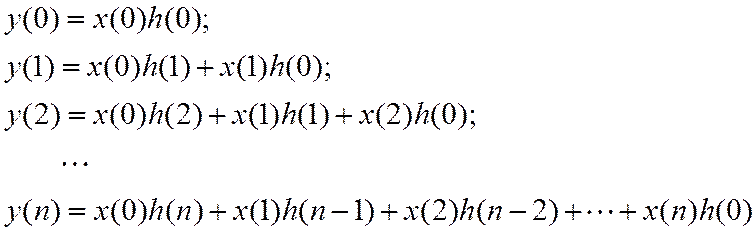
Пример 1.   Вычислить реакцию ЛДС по формуле свертки.

Импульсная характеристика имеет ненулевые отсчеты:

Входной сигнал имеет два ненулевых отсчета:

Вычисление выходного сигнала:

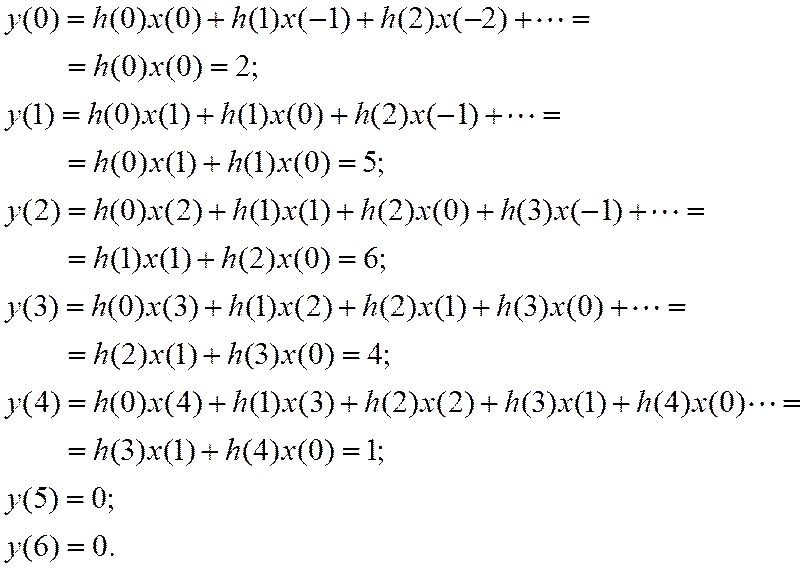
 Механизм вычисления свертки можно представить как последовательное вычисление сумм локальных произведений двух последовательностей: импульсной характеристики и воздействия. При этом одна из последовательностей фиксирована, а другая зеркально отражается относительно оси ординат и скользит слева направо по оси времени. В случае использования (7) фиксирован сигнал, а в (8) – импульсная характеристика.

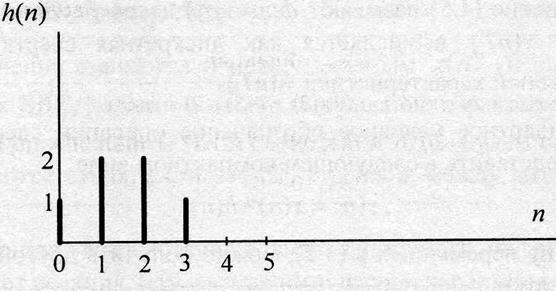
Рис. 4.4.

Рис.4.5.

            

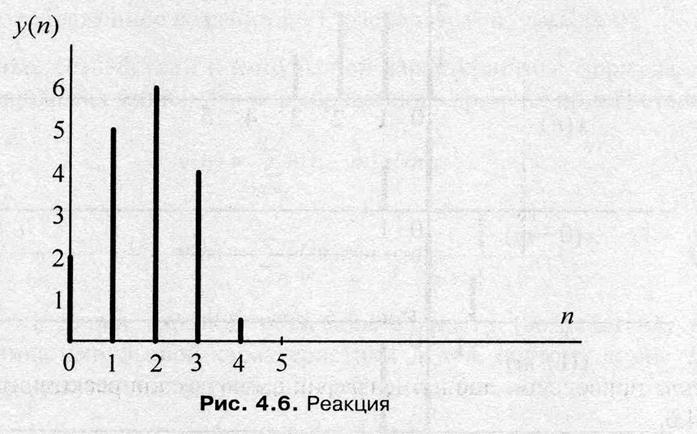
Рис.4.6.

Выводы:

• Если длительность импульсной характеристики и (или) воздействия бесконечны, то длительность реакции тоже бесконечна.
• Если длительность воздействия равна , а длительность импульсной характеристики равна , то длительность реакции равна

                                                                             

В последнем случае формула свертки приобретает вид

                                                                  

                                                                 

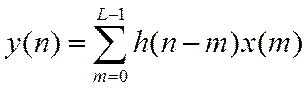
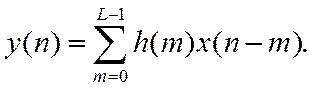
Рассмотренные выше операции дискретной свертки называют линейной (апериодической) сверткой. Другой вариант– апериодической (круговой) свертки будет рассмотрен позднее.

Пример 2. (Серг. 194).

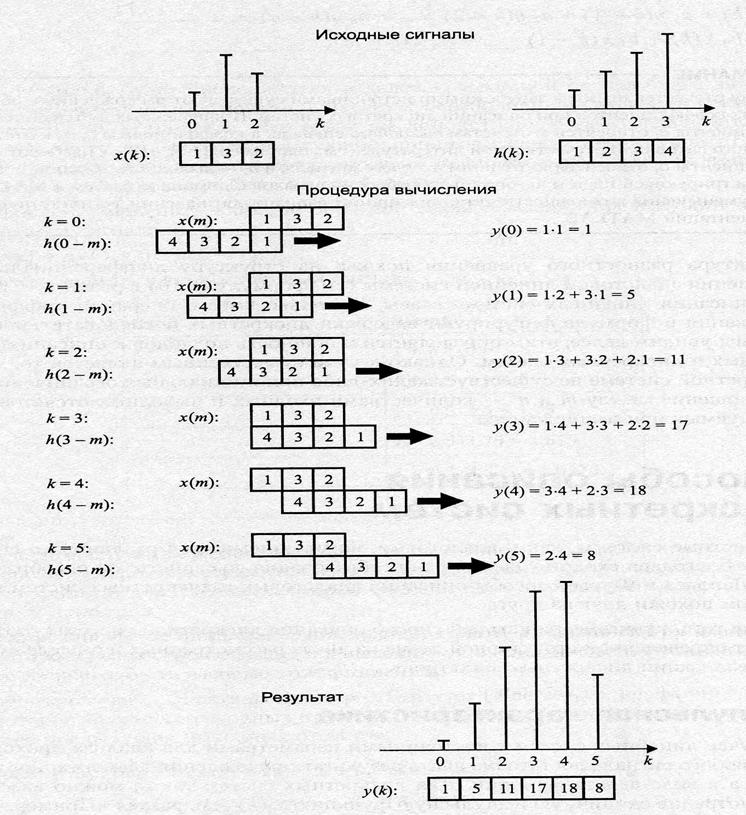
Рис. 4.1.

Вычисление дискретной свертки в MATLAB осуществляется с помощью функции CONV

Z=conv(x,y)