CONV Convolution and polynomial multiplication.
C = CONV(A, B) convolves vectors A and B. The resulting
vector is length LENGTH(A)+LENGTH(B)-1.
If A and B are vectors of polynomial coefficients, convolving
them is equivalent to multiplying the two polynomials.
See also DECONV, CONV2, CONVN, FILTER and, in the Signal
Processing Toolbox, XCORR, CONVMTX.
Свертку при конечной длине импульсной характеристики можно
рассматривать как матричное умножение. Одним вектором при этом служит ИХ,
другим – набор отсчетов входного сигнала![]() ,
определяемый как
,
определяемый как
![]()
Считая импульсную характеристику вектором-столбцом,
выражение для ![]() -го отсчета можно записать
-го отсчета можно записать
![]()
При расчете разных отсчетов используются соответствующие
векторы ![]() . Для получения всего выходного сигнала
отдельные строки
. Для получения всего выходного сигнала
отдельные строки ![]() объединяются в матрицу
объединяются в матрицу
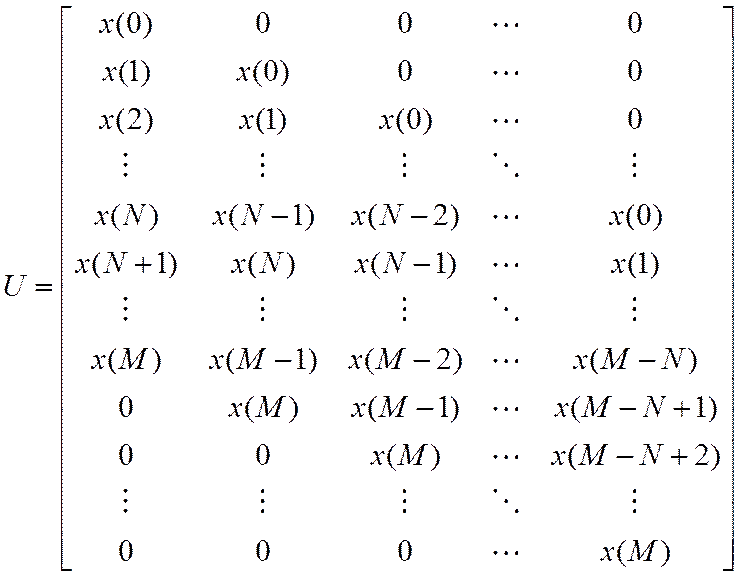
Эта матрица называется матрицей свертки. Выходной сигнал
получается![]() .
.
В MATLAB вычисление матрицы свертки осуществляется с помощью команды CONVMTX:
U=convmtx(x,n), x – вектор входного сигнала, n – длина импульсной характеристики.
CONVMTX Convolution matrix.
CONVMTX(C,N) returns the convolution matrix for vector C.
If C is a column vector and X is a column vector of length N,
then CONVMTX(C,N)*X is the same as CONV(C,X).
If R is a row vector and X is a row vector of length N,
then X*CONVMTX(R,N) is the same as CONV(R,X).
Разностное уравнение
В общем случае для ЛДС, работающих в реальном времени, соотношение «вход-выход» описывается уравнением
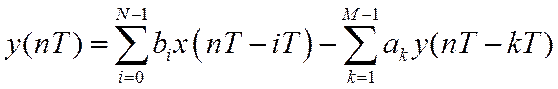
Для нормированного времени
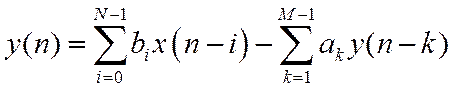
РУ имеет аналогию с ДУ линейной аналоговой системы
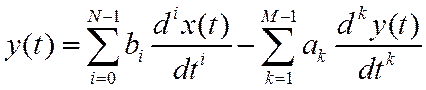
РУ решается методом прямой подстановки.
Нерекурсивные ЛДС
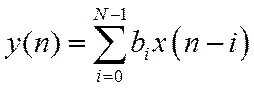
Текущий отсчет выходного сигнала определяется только N отсчетами воздействия: текущим и N-1 предыдущими. Порядок =N-1.
ИХ нерекурсивных ЛДС конечны è КИХ-системы.
Пример.
Дано РУ нерекурсивной ЛДС
![]()
Определить ИХ.
По определению ИХ
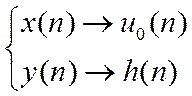
Тогда РУ запишется в виде
![]()
Вычислим отсчеты ИХ методом прямой подстановки
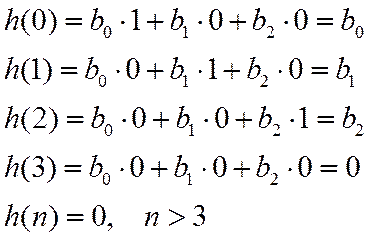
Результат можно обобщить
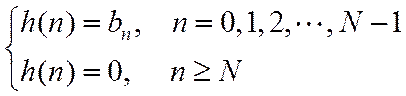
Т.о., ИХ нерекурсивной ЛДС имеет конечную длину. Ненулевые отсчеты ИХ совпадают с коэффициентами РУ.
Рекурсивные ЛДС
Описываются (17), в котором хотя бы один коэффициент ![]() .
.
Текущий отсчет выходного сигнала определяется не только текущим и предыдущими отсчетами воздействия, но и М-1 отсчетами выходного сигнала (ОС). Порядок =Max[(N-1,M-1)].
ИХ нерекурсивных ЛДС бесконечны è БИХ-системы.
Пример.
Дано РУ рекурсивной ЛДС
![]()
Определить ИХ.
По определению ИХ
![]()
Воспользуемся методом прямой подстановки
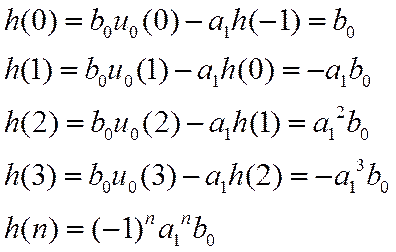
Устойчивость ЛДС
Определение: ЛДС устойчива, если при ограниченном воздействии отклик также ограничен.
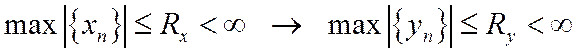
2 критерия: по импульсной характеристике и по Z-изображению.
Критерий устойчивости ЛДС
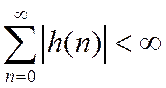
Доказательство:
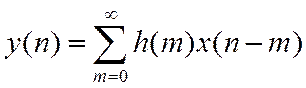
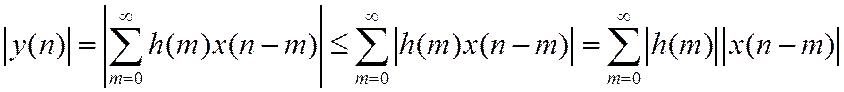
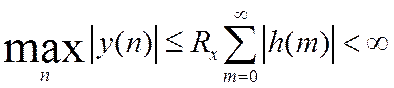
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.