Анализ возникновения структурного шума. Решение системы линейных алгебраических уравнений, формирование вектора правой части при линейной нагрузке

1. ВВЕДЕНИЕ

В данном курсовом проекте рассматриваются основные задачи, методы решения различных уравнений и прочие вопросы численной технологической механики.

Численная технологическая механика – это отдел механики, изучающий методы поведения и моделирования свойств конструкций, материалов конструкций и их элементов при их контакте с рабочими средами и участии в различного рода технологических процессах, включая эксплутационные. При этом к задаче обеспечения этих свойств состояния относятся: механические, физические, химические параметры материалов конструкций и рабочих тел.

В теоретической части работы особый акцент сделан на рассмотрении задачи акустики, а именно, на анализе возникновения структурного шума. Дифференциальное уравнение, описывающее этот процесс, относится к уравнениям эллиптического типа.

Практическая часть посвящается формализации решения системы линейных алгебраических уравнений, особое внимание уделяется формированию вектора правой части при линейной нагрузке. Для рационализации процесса решения составляется программа умножения матриц и векторов, так как при решении  системы ЛАУ эта процедура используется наиболее часто. Программа прилагается к материалам, изложенным в практической части.

2. Теоретическая часть

2.1. Дифференциальные уравнения и их решения для волновых

процессов в газообразных и жидких средах

        Волновые процессы в газообразных и жидких (акустических) средах наиболее важны для акустики, так как именно в этих средах происходят их взаимодействие, распространение и восприятие человеческими слуховыми органами или специальными приборами.

        Звуковые волны в акустических средах возникают и передаются в виде деформаций сжатия и растяжения этих сред, происходящих на фоне статического давления Р₀. Изменение этого давления при прохождении звуковой волны называется звуковым давлением Р, обычно Р<<P₀.

        Звуковое давление вызывает изменение объема элементов акустической среды. При этом восстанавливающей силой, необходимой для существования волнового движения, является сопротивление, которое газ или жидкость оказывают сжатию. Характерным обстоятельством для акустической среды является то, что изменение формы объема элемента такой среды (например, из прямоугольника в параллелограмм) сопротивления не оказывает. Таким образом, изменение объема акустической среды является единственной причиной возникновения и распространения звуковой волны в акустической среде. Следовательно, звуковая волна в акустической среде является, по сути, волной давления. Из сказанного ясно, что основным параметром, характеризующим звуковую волну в акустической среде, является звуковое давление.

        Дифференциальное уравнение, описывающее изменение звукового давления Р в пространстве и времени в произвольной акустической среде имеет вид:

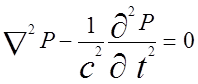.                 (1.1)

Где t – время; c – скорость распространения звуковой волны; P – функция координаты и времени; Ѳ – дифференциальный оператор, называемый Лапласианом, определяет концентрацию величины Р; если величина Ñ²Р отрицательна, то имеет место концентрация (увеличение) давления, еслиÑ²Р положительна, значит давление уменьшается.

        Физический смысл волнового уравнения заключается в том, что если в некоторых точках среды имеет место повышение давления, то оно стремится уменьшиться.

        Как было сказано выше, мы будем иметь дело главным образом с периодическими процессами, временная зависимость которых определяется множителем (может быть взят также множитель), где w=2pf – круговая частота; f – циклическая частота. Подставляя этот множитель в уравнение (1.1) и, дифференцируя по t, получим:

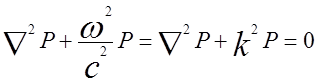.      (1.2)

        Здесь Р – функция координаты; k=w/c=2p/l - волновое число акустической среды (l - длина волны звука). Этот параметр очень важен в акустике. Например, для сравнения размеров излучателей или препятствий для звука используют обычно их волновой размер kl (l – линейный размер). Если kl=wl/c=2pl/l<<1, размер излучателя или препятствия l мал по сравнению с длиной волны l. Наоборот, если kl>>1, этот размер велик по сравнению с длиной волны.

        Иногда используют оператор Гамильтона …²=Ѳ+k². В этом случае волновое уравнение приобретает предельно простой вид: …²Р=0.

        Для решения задач акустики используют различные системы координат в зависимости от геометрии исследуемых устройств и конструкций.

        В прямоугольной системе координат (x, y, z) Лапласиан равен:

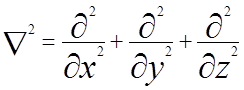;                                               (1.3)

В цилиндрической системе координат (r, j, z):

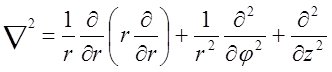;                                         (1.4)

В сферической системе координат (r, q, j):

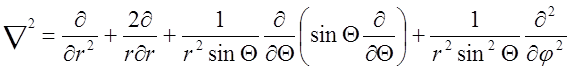.    (1.5)