Решение уравнения (1.2) в прямоугольной (декартовой) системе координат удобно искать в виде экспоненциальных функций, в цилиндрической системе – в виде функций Бесселя, в сферической – в виде полиномов Лежандра.
Простейшим случаем волнового уравнения является одномерный вариант прямоугольной системы координат. Пусть в этом случае плоская волна распространяется вдоль координаты х. Тогда волновое уравнение принимает вид:
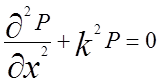 (1.6)
(1.6)
где Р – функция только координаты х.
Мы
ограничимся рассмотрением решения только этого случая волнового уравнения, имея
ввиду, что основные результаты справедливы и для более сложных координатных
ситуаций. Учитывая принятую выше зависимость Р от t в виде ![]() , решение уравнения (1.6) можно представить
в виде:
, решение уравнения (1.6) можно представить
в виде:
P(t, x)=P![]()
![]() =P
=P![]() (1.7)
(1.7)
Где Р – амплитуда звукового
давления, ![]() - его фаза.
- его фаза.
Мгновенное
распределение амплитуды Р вдоль оси х можно определить вещественной частью
множителя ![]() , т. е. сos(kx).
Расстояние между ближайшими точками этого распределения с одинаковой фазой,
например максимальными значениями амплитуды Р, называется длиной волны l.
, т. е. сos(kx).
Расстояние между ближайшими точками этого распределения с одинаковой фазой,
например максимальными значениями амплитуды Р, называется длиной волны l.
Направление
распространения амплитуды волны вдоль координаты х можно проследить с помощью
фиксированного постоянного значения фазы ![]() . Если в
значении фазы перед kx стоит знак «+», то по прошествии некоторого времени Dt для сохранения
постоянства фазы координата х должна быть уменьшена. Иными словами, в этом
случае волна перемещается в сторону отрицательных значений координаты х. При
знаке «-» перед kx постоянство фазы сохраняется при увеличении
координаты х. Следовательно, волна перемещается при этом в положительном
направлении.
. Если в
значении фазы перед kx стоит знак «+», то по прошествии некоторого времени Dt для сохранения
постоянства фазы координата х должна быть уменьшена. Иными словами, в этом
случае волна перемещается в сторону отрицательных значений координаты х. При
знаке «-» перед kx постоянство фазы сохраняется при увеличении
координаты х. Следовательно, волна перемещается при этом в положительном
направлении.
Таким
образом, множитель ![]() означает волну,
распространяющуюся в сторону положительных значений координаты, множитель
означает волну,
распространяющуюся в сторону положительных значений координаты, множитель ![]() определяет волну, распространяющуюся в
противоположном направлении.
определяет волну, распространяющуюся в
противоположном направлении.
При распространении волны давления каждый элемент среды претерпевает периодические сжатие и расширение. Очевидно, что граничные поверхности этих элементов совершают также периодические ( с той же частотой) перемещения вдоль направления распространения волны. Таким образом, при распространении звуковой волны частицы среды совершают периодические перемещения с некоторой колебательной скоростью v(t, x). Значение этой скорости в общем случае определяется уравнением
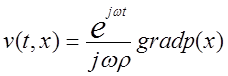 .
(1.8)
.
(1.8)
где r - плотность среды; grad – дифференциальный оператор; для плоской волны, распространяющейся вдоль координаты х, grad p(x)=¶/¶x.
Следовательно, для этого простейшего случая
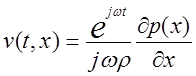 (1.9)
(1.9)
Величина grad Р называется градиентом звукового давления, так как он определяет перепад звукового давления между соседними точками среды. Колебательная скорость v(t, x) также удовлетворяет волновому уравнению, т. е.
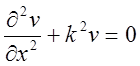 (1.10)
(1.10)
где V – функция координаты.
Значение v(t, x) равно
v(t, x)=V*![]() , (1.11)
, (1.11)
где V – амплитуда колебательной скорости.
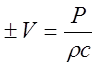 ,
(1.12)
,
(1.12)
из которого видно, что для получения информации о звуковом давлении можно использовать измеритель колебательной скорости v. Знак перед v выбирается в соответствии с направлением распространения волны.
Величина rс называется акустическим сопротивлением среды.
Из уравнения (1.12) следует также часто используемая электромеханическая аналогия, согласно которой колебательная скорость v аналогична электрическому току, звуковое давление Р – электрическому напряжению, а акустическое сопротивление rс – электрическому сопротивлению. С учетом сказанного легко заметить, что уравнение (1.12) аналогично закону Ома.
Практически важной характеристикой звуковой волны является количество энергии, заключенной в единице объема среды. Эта величина, называемая плотностью энергии w, равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.