Анализ возникновения структурного шума. Решение системы линейных алгебраических уравнений, формирование вектора правой части при линейной нагрузке, страница 8

Одной из проблем возникающих при решении задач нелинейного поведения конструкции является разработка достаточно точного и устойчивого метода сведения нелинейной задачи с начальными и граничными условиями к последовательности нелинейных краевых задач относительно пространственных координат. Реализация таких задач требует обеспечения точности в каждой точке объема материала конструкции, что существенно уменьшает шаг решения по времени. В то же время малый шаг увеличивает суммарную погрешность. Дополнительным условием обеспечения устойчивости решения динамических задач может служить то, что после достижения максимального значения деформации-перемещений ε_max(t) в амплитуде первого максимума дальнейшее нарастание производной по времени-скорости или ускорения можно ограничить их рост принудительным выполнением неравенства V_max(t)≤ ε_max(t)∙ C₀, где C₀ – скорость звука материала конструкции.

АЛГОРИТМ ПРОГРАММ

Формирование матрицы Якоби

Печать введенных исходных данных

Чтение введенных исходных данных

Ы

		Вычисление функций формы элемента и ее производных

Последовательность решения  в задаче определения уровня структурного шума на транспортных машинах:

I. Определение собственных частот и форм колебаний замкнутого воздушного объема салона. Для низших форм строятся изолинии давления. Анализ вида их  распределения предполагает внесение требуемых изменений геометрической формы салона при выявлении роста интенсивности в опасной зоне (у головы водителя).

Подробно анализируются собственные значения выделенных отдельно элементов машин: пола, крыши, дверей, стекол. Необходимо отметить, что поскольку исследования последних элементов машин не могут быть проанализированы экспериментально способом выделения из основной части машины, то их анализ производится путем отклика на принудительную вибрацию, рост амплитуд которой говорит о частотах возбуждений совпадающих с собственными. Таким образом, возможна коррекция полученного численного решения, что оправдано, для таких весьма сложных в моделировании деталей.

II. Анализ поля структурного шума в салоне. Проведение динамического анализа – определение амплитудно-частотной вибрации панелей от источников возбуждения. Решается уравнение [M]{U¨} + [H]{U´} + [K]{U} = {F}, в котором входным вектором  нагрузок является вектор виброскоростей и виброускорений характерных точек-узлов крепления панелей. Входными данными для расчета виброскоростей по каждому элементу конструкции (панелей и т.п.) принимаются согласованные по времени и экспериментально измеренные типовые зависимости виброускорений рамы и пола кузова (желательно в точках-узлах креплений панелей) от частоты возмущающих усилий в диапазоне исследования. Физико-математические характеристики конечномерной модели каждой панели определяются их изменением – "подгонкой" до совпадения не менее чем двух резонансных пиков, полученных экспериментально и соответствующих ее собственным частотам. Сформированные таким образом параметры и матрицы дифференциальных уравнений движения считаются достоверными. Как обосновано ранее, до значений частот менее f_н = 230-320 Гц (усредненному до ~250 Гц), расчет структурной составляющей нужно проводить только по формуле

[M]{U¨} + [K]{U} = {F}.

При этом для расчета используется нестационарное уравнение статики

[K]·{∆(t)} = {F(t)}_г, при 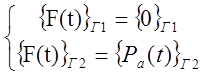,  и Г = Г₁ + Г₂,

где [K] - матрица жесткости воздушной среды салона, {∆(t)} - вектор-форма деформирования панелей-границ салона на Г₁ от вибрации, создающий {F(t)}_г - вектор модифицированных нагрузок салона, т.е. при "нулевом значении" сил {0}_Г1, {P_а(t)}_Г2 = ∑ⁿ∫^Г1 P_аcos(t)dГ₁ - акустический вектор звукового давления на срезе - открытой поверхности Г₂ салона, части полного вектора {F(t)}_г  на всей поверхности Г.