Анализ возникновения структурного шума. Решение системы линейных алгебраических уравнений, формирование вектора правой части при линейной нагрузке, страница 11

Октавный уровень: по 2-й октаве 91.67 дБ; по 3-й 103.7.

3.3. Формирование исходных данных, расчет геометрических

характеристик панели¾двери задка

Для двери задка необходимо составить расчетную схему из набора стержней (см. Рис.), сосчитать их геометрические характеристики поперечных сечений. Исходные данные для расчета взять табличные. Просчитать значения звукового давления по данным пакета ANSYS и сопоставить результаты.

Таблица 4.1.

Зависимость уровня звукового давления на рабочем месте водителя от

частоты возмущающего усилия в ди­апазоне от 31.5 до 140 Гц для панели N₀ За

Наиме­нова­ние панели	Характер нагружения  виброускорение по направлениям XYZ  (Рис. 4. 1,4. 6)		Уровень звуково­го дав­ления, ДБ
	Частоты, Гц fx     fy     fz	Амплитуды перегрузки, м/с2 Ах    Ay   Az
Дверь задка с колесом	41.220 41.220 41.220	0.3800 0.3800 0.3800	81.44
	51.600 51.600 51.600	0.6600 0.6600 0.6600	86.55
	57.900 57.900 57.900	0.6000 0.6000 0.6000	89.47
	77.200 77.200 77.200	2.4300 2.4300 2.4300	93.21
	81.800 81.800 81.800	2.3800 2.3800 2.3800	93.68
	91.700 91.700 91.700	1.3200 1.3200 1.3200	94.18
	103.00 103.00 103.00	2.5800 2.5800 2.5800	95.27
	115.00 115.00 115.00	1.9000 1.9000 1.9000	96.05
	122.00 122.00 122.00	1.4800 1.4800 1.4800	96.39
	130.00 130.00 130.00	1.5000 1.5000 1.5000	96.57
Суммарный уровень звук. давления для диапазона 31.5+140 Гц: 103. 9

Октавный уровень: по 2-й октаве 91,67 дБ; по 3-й 103,7.

Определение геометрических характеристик

поперечных сечений стержней

           1.                                         2.                                     3.

                        у                                                                                    у

                                                                        у

       z                                8     z                                        z                                    20 

                                                                                       2

                     60         t=1.5                         200                                   25           t=1,2

Определение геометрических характеристик сложных поперечных сечений стержней основывается на разбиение сложной фигуры на более простые части, центры тяжести которых известны. Затем для каждой части отмечается положение центра тяжести С_i  и его координаты у_i, z_i относительно некоторой произвольно выбранной координатной системы.

Координаты центра тяжести всей фигуры относительно оси z, y определяем по формулам: ,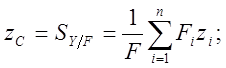

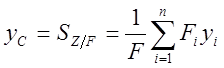где F, F_i - площади фигуры и ее частей.

Вычисляем для собственных осей элементов площади фигуры осевые и центробежные моменты  инерции.

Центробежные моменты инерции элементов фигуры относительно ее центральных осей равны нулю, если в этих элементах имеется хотя бы одна ось симметрии (параллельная оси у или z).Затем определяются моменты инерции относительно центральны осей у_с, z_с всей фигуры. Так как они параллельны осям z_i, y_i, проходящим через центр тяжести каждого элемента фигуры, то можно воспользоваться формулами, позволяющими определить осевые и центробежный моменты инерции для произвольных осей, если известны ранее найденные моменты инерции для центральных осей z_i, y_i  каждого элемента:

,     ,    .

где ,   .

Здесь z_ic, y_ic - координаты центров тяжести частей площади фигуры в системе z_c, y_c, а по абсолютной величине соответственно расстояние между осями y_i, y_c и z_i, z_c.

Общая величина осевых и центробежного моментов инерции фигуры находится суммированием моментов инерции отдельных частей фигуры: