Анализ возникновения структурного шума. Решение системы линейных алгебраических уравнений, формирование вектора правой части при линейной нагрузке, страница 9

Решение уравнения [K]·{∆(t)} = {F(t)}_г можно выполнить двумя способами:  ведением на границе открытой поверхности объема элементов, учитывающих протяженность R∞ пространства с физико-механическими свойствами воздушной среды или учетом возможности стока давления от части границы в это упругое полупространство. В первом случае в уравнении матрица жесткости среды объема салона выполняется элементами описания части примыкающего пространства, содержащими полубесконечные функции на границе вида

N_j = N_j(s) ∙N_j(η), где N_j(s) = L_j (s)∙e^-(s-s´)/H∙e^u, N_j(η) = L_j (η),

где L_j (s), L_j (η) ¾ обычные полиномы Лагранжа, а Н - линейный параметр скорости затухания или расстояние затухания. Здесь девятиузловой конечный элемент пространства определяется в локальной системе координат ξ и η. Координата ξ простирается в бесконечность и совпадает с направлением координаты s, которая связана с глобальной системой X,Y соотношением ds² =dX² + dY², то есть может и не совпадать с направлениями X и Y. Для узла j начальное значение координаты s равно s_j = s^', которое входит в степень выражения N_j(s). Другой сомножитель  (e^u) функции формы для комплексных узловых значений равен u = iks и отражает условие распространение волн давления. Его падение на расстояние s за время t учитывается отношением u = -(t-s/c₀) при скорости звука в воздухе c₀. Так как моментное значение частоты звукоизлучения (демпфирования панелей) находится в диапазоне 1,5¸300 Гц, то полагая минимальным время распространения за один период колебаний, можно считать конечным значением пробега звуковой волной расстояния R∞=Н=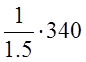м/с ≈ 226,7¸1,13 м/с, а продолжительность общего времени прохождения самого дальнего расстояния звуковой волной равно t_∞ ≈ 0,67 с.

С помощью этих функций формируются элементы матрицы жесткости части полупространства со свойствами воздушной среды:

[K]^e = 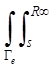[N(s)]·[N(η)]dV,

где Г_е - часть поверхности открытого пространства, R_∞ - известно, dV = dГ·ds - элементарный объем, равный произведению элементарной площади на расстояние ds.

После интегрирования эта матрица жесткости дополняет систему уравнений. Тогда решение уравнения, проводимое с учетом преобразования нулевого правого вектора на ненулевой вектор модификации {F(t)}', обусловленный наличием начальных значений перемещений {∆(t)}, выполняется однократно.

Во втором способе уравнение [K]·{∆(t)} = {F(t)}_г решается в два этапа: на первом определяется начальное значение вектора давления {P_а(t)}_0Г в зоне открытой части границы объема Г, но для закрытого варианта. Очевидно, что это давление будет максимальным для открытой границы. На втором этапе этот вектор с амплитудой полученного давления дополняется функциями, учитывающими сброс давления в полупространство в виде

{F(t)}" = {P_а(t)} · е^-Н",

где Н" = (s-s')/Н и соответствует предельному расстоянию R∞.

Поскольку у геометрической формы большинства салонов транспортных машин существуют плоскости симметрии, то решение справедливо выполнять для них в плоской постановке. В процессе расчета определяются компоненты тензора напряжений (давление р₀) упругой воздушной среды при ее деформировании перемещениями {∆(t)}, со скоростями движения окружающих стенок, испытывающих вибрацию, т.е. в различные моменты времени. Тогда базовая модель алгоритмов программ, обладая такими решениями, может претендовать на достоверность и полноту описания физического процесса явления структурного шума. Тем не менее, в качестве дополнительного расчета возможно вычисление стандартным методом логарифмического суммирования по формуле определения звукового давления в характерной точке салона - у головы водителя от дискретного набора источников - заданного количества узлов расчетной модели панели конструкции: дверей, крыши, пола и т.д., по известной формуле для суммарного уровня звукового давления:

L_сум = 10 lg10^0,1Li,

Для использования в конечномерных представлениях с учетом акустики ближней зоны, формула изменена и дополнена, и имеет вид:

L_s = 10 lg10^0.1Li(t),