Уравнения параболического типа, теория диффузии и практическое составление матрицы инерции четырехугольного элемента с использованием метода редукции

МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ РОССИИ

Балтийский Государственный Технический Университет

«ВОЕНМЕХ» им. Д.Ф. Устинова

кафедра механики деформируемого твёрдого тела

КУРСОВАЯ РАБОТА

по численной технологической механике

Диффузия.

Формирование матрицы МАССЫ

На основе разработки

составного из треугольных четырехугольного элемента

                                             Студент:

                                                Группа: Б

Проверил: Санников В. А.

Санкт-Петербург

2001

 

Содержание.

1.  Введение.                                                                                                3

2.1  Уравнение массопереноса                                                                   4

2.2.Задачи диффузии                                                                                  7

2.3.Задачи  конвекции  и  диффузии                                                         8

2.4.Нелинейная  диффузия                                                                         9

3.1.Формирование  матрицы  жесткости  элементов  составных   

элементов повышенной  точности  методом  редукции.                        10

3.2. Решение системы  линейных  уравнений с  матричной  матрицей

коэффициентов .                                                                                          15

4.   Заключение.                                                                                           19 

5. Список   литературы        20

1. Введение

Цель  данной курсовой  работы заключается в  закреплении полученных  знаний, как теоретических, так и практических .В  этой  работе  рассматриваются   уравнения   параболического  типа,  теория  диффузии   и практическое  составление  матрицы  инерции   четырехугольного  элемента с использованием  метода  редукции ,  решение  системы  линейных  уравнений  с  ленточной   матрицей  коэффициентов.

В  теоретической части  основой   вывода     служит  уравнение   массопереноса ,к которому в результате  преобразований применяют   метод   Галеркина, и пренебрегая конвективными  членами  в  полученных  уравнениях для получения уравнения диффузии.  В  практической  части  рассмотрена  схема составления  матрицы  инерции  по  аналогии с  матрицей  жесткости  элемента. На этом примере, показано использование метода  редукции (удаление  центрального  узла в прямоугольном  элементе). Приводится программа  для решения системы  линейных  уравнений  с   использованием  ленточной  матрицей  коэффициента. Вид  уравнения АХ= R,  где А — ленточная матрица коэффициентов порядка M; R — матрица правых частей системы уравнений размером М  N.

2.1.  Уравнение массопереноса

Рассмотрим  произвольный  объем  жидкости  в  моменты  времени  t и t + (рис 1  ). Количество   растворенного вещества, втекающего и вытекающего из этого объема, определяется выражением

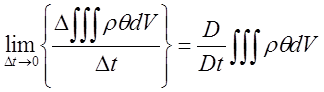                                                                                 ( 1 )

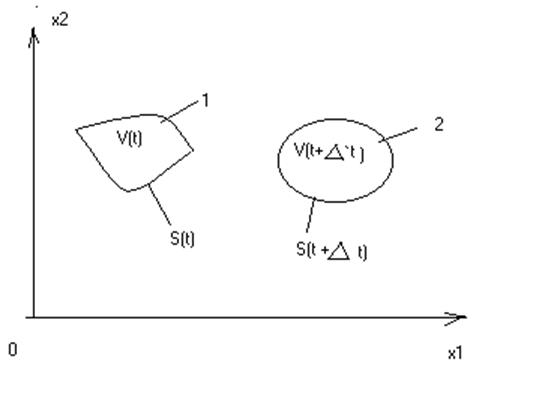             Рис.1 . Объем в моменты времени t (1) и t+  (2)

Уравнение (  ) характеризует изменение количества вещества, содержащегося в объеме V.

Если общую массу контрольного объема можно считать постоянной (т. е. изменение концентрации не влияет на полную массу), то

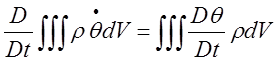  ,                                                                                      (2)

где D/Dt— полная производная, включающая в себя компоненты скорости  в направлениях  .

Скорость подвода вещества через границу за счет потока вещества и внешнего подвода можно записать следующим образом:

 ,                                                                                                    (3)

где р — внешний подвод (скорость распределенного подвода, приходящаяся на единицу массы); — нормальный поток через границу.

Уравнение установившегося режима с учетом зависимостей ( 2) и ( 3) можно выразить так:

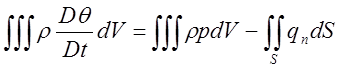                                                                                  (4)                 

Применяя теорему Гаусса, преобразуем поверхностный интеграл в уравнении  (4) в объемный. Тогда вместо уравнения ( 4). Получим