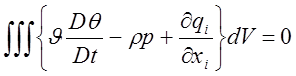Уравнения параболического типа, теория диффузии и практическое составление матрицы инерции четырехугольного элемента с использованием метода редукции, страница 2

                                        (5)

Поскольку объем произволен, то согласно выражению (5)

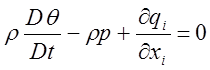                                                   (6)

Уравнение (6 ) есть основное уравнение задачи.

Для молекулярной диффузии связь между  и  :

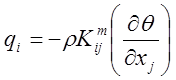                                                           (7)

где  -коэффициенты  молекулярной диффузии .

Обычно предполагается, что главные направления составляющих  совпадают с направлениями осей. Это дает ортотропные коэффициенты молекулярной диффузии

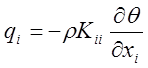                                                                (8)

Уравнение равновесия ( 6 ) можно записать тогда через значение концентрации:

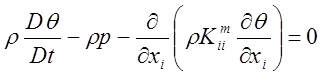    или                              (9)

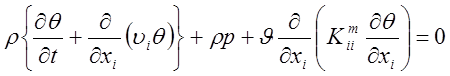                          (10)

Турбулентность обычно учитывается путем представления переменных в уравнении ( 9) в виде суммы средних величин и пульсаций:

  ;                                                      (11)

где    и -средние значения скоростей и концентрации;  и - соответствующие пульсации.

Средине значения определяются следующим образом:

Отсюда вытекает, что

 ,        ,   или                         (12)

Подставим выражения (11) для мгновенных значений величин в уравнение массопереноса (9). В результате будем иметь

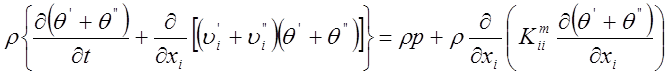              (13)

Интегрируя равенство  ( 13 ) по всей области, получаем :

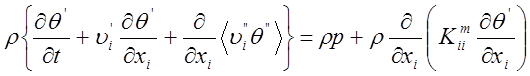                                      (14)

Пульсационный член в уравнении (14 ) обычно представляется в виде  :

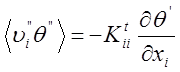                                                                                                        (15)

где— эмпирические коэффициенты ( коэффициенты вихревой диффузии).

.

Коэффициент молекулярной диффузии можно сложить с и получить полный коэффициент диффузии. Таким образом, уравнение ( 14 ) можно записать в виде

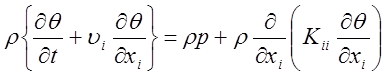          (16)

В уравнении (16) для упрощения у средних величин опущены штрихи. Источники и стоки в рассматриваемом объеме представлены в уравнении (16 ) величиной р. Обычно желательно выделить в р член, учитывающий влияние концентрации, т. е.  Представить  p в виде :

  ;                                                                                                             (17)

где f — распределенный источник;  — постоянная, учитывающая влияние концентрации.

Уравнение (17 ) описывает случай линейного закона для  концентрации, который очень удобен для математического моделирования. В ряде случаев принимают экспоненциальный закон  спада концентрации по времени:

   ,                              

 где  - начальная концентрация;  — константа.

В дальнейшем ограничиваются рассмотрением лишь линейного закона концентрации.

   Поглощение (абсорбцию  вещества) на границе можно представить, выразив

поток вещества через величины концентрации на внешней стороне границы

и на границе . Это дает

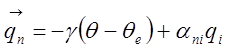                                                                                                (18)

где— коэффициент абсорбции на границе;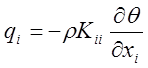 

Точечный сток можно определить как

,                                                                                                        (19)

где— сток в точке ;  — дельта-функция (равна 1 для координат и 0 для всех остальных точек).

. Используя в качестве веса для уравнений ( 16 ) вариацию , можно записать

вариационную формулу метода Галеркина и выразив   через  :

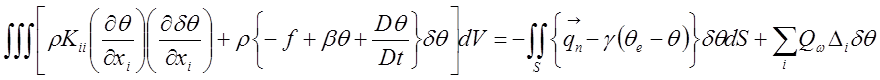(20)

Можно получить задачу  для двумерной области .  Тогда уравнение будет  выглядеть:

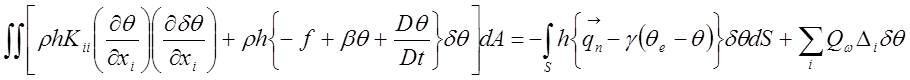 (21)

где h — глубина.

В пределах каждого элемента представим  как

                                                                                                                     (22)

где ф () — интерполяционная функция;  — вектор узловых неизвестных.

После подстановки в уравнение (21 ) для каждого элемента получим

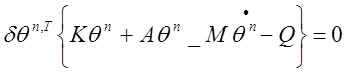  ;                                                                              (23)

где

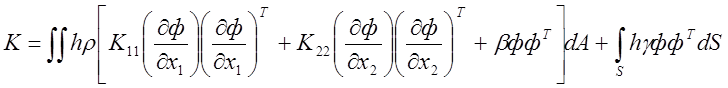 ;                        (24)

  ;

  ;

 

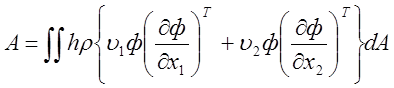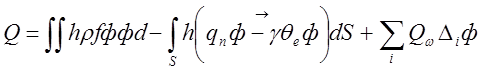
Для  всей  области  :

  .                                                                                                   (25)

2.2.  Задачи диффузии

Рассмотрим случай чисто диффузионной задачи, для чего пренебрегают  конвективными членами в выражении (25  ). Тогда

  .                                                                                                  (26)      

Этот случай наблюдается при отсутствии потока вещества (например, температурная диффузия в твердом теле, изменение концентрации в спокойной воде). Матричное уравнение (26  ) может быть проинтегрировано по времени