Анализ прочности метаемых тел при импульсном нагружении

 АНАЛИЗ ПРОЧНОСТИ МЕТАЕМЫХ ТЕЛ ПРИ ИМПУЛЬСНОМ НАГРУЖЕНИИ

Д.П. Александров*, В.А. Санников** (*СПб государственный технический университет, **Балтийский гос. технический университет, СПб, Россия)

Использование тепловых импульсных машин для метания тел из стволов различного калибра не утрачивает своей актуальности. Анализ газодинамических процессов при выстреле - выталкивании тела из орудия и взаимодействия системы метаемое тело-ствол оказывает существенную помощь для отработки и развития новых конструкторских схем направляющих и метаемого тела, а также разработку мероприятий по подавлению вспышки и воздушной волны при выстреле.

В основу положена схема численного интегрирования одномерных дифференциальных уравнений внутренней баллистики, описывающих динамику пороховых газов в частных производных при постоянном поперечном сечении [2]:

Уравнение движения газа записывается в лагранжевой форме:

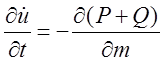            (1)

где —скорость, t—время, т—масса на единицу площади, Р—давление и Q—искусственная вязкость для «размазыва­ния» ударных волн [I]. Уравнение сохранения энергии имеет вид

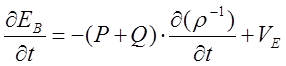                    (2)

где Е_В—внутренняя энергия, отнесенная к единице массы газа, r^-1=1/r—удельный объем (величина, обратная плот­ности) и V_E — скорость поступления энергии в газ за счет сгорания заряда. Движение снаряда в стволе описывается уравнением

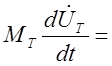              q_д×S  .                         (3)

Здесь М_Т—масса снаряда, —его скорость, q_д—давление газа на основание снаряда и S — площадь поперечного сечения ствола.

Уравнение (3) при решении задачи определения напряженно-деформированного состояния (НДС) приобретает вид

[M(t)]d{(t)}/dt + [K(t)]{U(t)} = {F(t)}  ,         (4)

где: [М(t)], [K(t)] - матрицы массы, жесткости метаемого тела; {F(t)}v–вектор столбец нагрузок вызванных внутренними массовыми силами или {F(t)}т –тепловыми изменениями в объеме V;{q(t)}_S1 – распределенными поверхностными нагрузками (например q_д) на поверхности S₁; {U}_S2 –перемещениями на S₂. В целом для общего вектора {F(t)}= {F(t)}v + {F(t)}т + {q(t)}_S1 .

Решение уравнений (1) и (3), с учетом уравнения состояния (3), описывающих функции переменные в пространстве и вре­мени, выполняется методом конечных элементов, а (4) - методом Бубнова, индифферентного к граничным условиям, что соответствует характеру рассматриваемых процессов

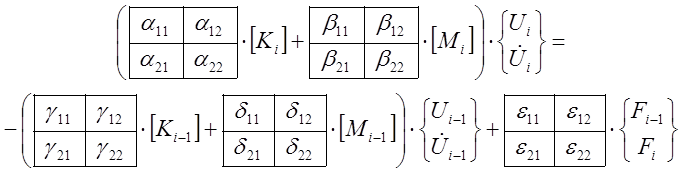 (4,а)

Векторы перемещений U_i-1искоростей  в начальный момент времени, при t=t_н=0, равны значениям U(0) и (0); {F(t)}- текущий вектор нагрузки; i- шаг итерации прямого решения, a a₁₁, a₁₂, b₁₁, b₁₂, g₁₁  и т. д. - коэффициенты рекуррентного со­отношения, учитывающие координату времени на исследуемом отрезке D(t_i); [K]_i, [M]_i-1, F_i-1, F_i - матрицы и векторы параметров исследуемого объекта, размерностью n´n входящие в уравнение (1) на текущем и предыдущем шагах.

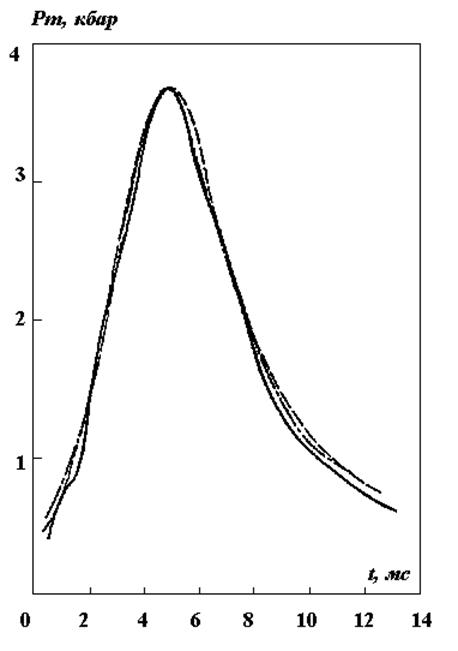
Для обоснования применимости МКЭ к расчету внутренней баллистики используются экспериментальные и теоретические данные, приведенные в работе [2]: длина камеры орудия Lо=100 см, площадь его поперечного сечения S=130 см², масса снаряда М_Т = 3,8×10⁵ г, полное расстояние, проходимое снарядом, L = 600 см. Порох (90% нитроцеллюлозы и 10% добавок) и состоит из цилиндрических зерен диаметром ØD=0,69 см и плотностью твердого вещества r_o =1,5 г/см³, полный вес заряда W= 9,0×10³ г.

Термическое уравнение состояния газа представляется в виде

Р×(V-b)=пRТ        ,                   (5)

где b»0,95 см³/г—объемная поправка; получающееся при сгорании 1 г нитроцеллюлозы количество газа п»0,04 грам-моль/г; R — газовая постоянная, равная ~83,15 бар×см³/ (граммоль×°К).

Процесс горения цилиндрических зерен пороха диаметром fD, где 0 £f£1 при сгорании пороха в окружающем газе, описывается эмпирическим законом

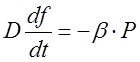     ,         (6)

где b—постоянная скорость горения [4]. Полагая процесс выгорания топлива как j = 1 — f², с учетом                       

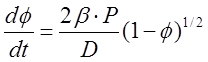                 ,           (7)

и получаемой скорости поступления энергии в газ равной  В=E₀ зависимость плотности газа от j  будет описывается формулой

r_o =Wj / [S(L+x)-(1-j)W/r_o],            (9)

где х=х(j)—расстояние, которое проходит снаряд под давлением.