Методика численного анализа задачи определения теплового состояния на основе формирования и решения уравнения теплопроводности методом конечных элементов

Министерство ОбразованиЯ РФ

БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КурсоваЯ работа

ПО ЧИСЛЕННОЙ ТЕХНОЛОГИЧЕСКОЙ МЕХАНИКЕ

ЗАДАЧА ОПРЕДЕЛЕНИЯ ТЕПЛОВОГО СОСТОЯНИЯ НА ОСНОВЕ

ФОРМИРОВАНИЯ И РЕШЕНИЯ УРАВНЕНИЯ

ТЕПЛОПРОВОДНОСТИ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Студентки .

Группа Б-

Проверил Санников В.А.

С-Петербург

-2002 г.-

СОДЕРЖАНИЕ:

Стр.

ВВЕДЕНИЕ        ……….………………………………………………………………………...4

1     Теоретическая часть         …………………………………………………………………..5

1.1     Численные методы решения краевых задач нестационарной теплопроводности. …..5

1.2     Формулировка основных соотношений при решении задачи нестационарной теплопроводности       …………………………………………………………………………..7

1.3     Численный анализ нестационарных полей температур в элементах конструкций с помощью МКЭ         ……………………………………………………………………………..9

2     Переход от дифференциальных уравнений к расчётной модели ………………………13

3     Применение изопараметрического квадратичного элемента для решения задач теплообмена     …………………………………………………………………………………15

4. Естественная система координат. Преобразования координат.Матрица Якоби ……….17

5.Алгоритм расчета Якобиана  ………………………………………………………………  19 6. ЗАКЛЮЧЕНИЕ………………………………………………………………………………21

7. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………………………………..21

ВВЕДЕНИЕ

В данной работе рассматривается методика численного анализа задачи определения теплового состояния на основе формирования и решения уравнения теплопроводности методом конечных элементов. В дальнейшем предполагается использование расчета для определения долговечности конструкций при термохимическом нагружении. При этом необходимо не только знать закономерности достижения предельного состояния, но и располагать данными о полях температур. Задачу об определении полей температур во всём объёме рассчитываемой на прочность детали в зонах локализации указанного фактора необходимо решать в кинетической, циклической, упругой  и упругопластической постановке.

Для анализа области применения разработанных на кафедре программах либо пакетах программ, применяемых на производствах, требуется приобретение навыков некоторых вычислений и анализа теоретических разработок, что и приведено в данной курсовой работе.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1  Численные методы решения краевых задач нестационарной теплопроводности

Для расчета на прочность конструктивных элементов, работающих в условиях термомеханического нагружения, необходимо последовательно определить нестационарные поля температур и по ним построить поля напряжений, упругих и упругопластических деформаций, характеризующие особенности деформирования в напряженных зонах конструкций.

Согласно постановке краевой задачи необходимо найти в трёхмерной области V, ограниченной замкнутой поверхностью S, тензорное поле Q(r), где r – вектор, определяющий положение произвольной точки внутри области V глобальной криволинейной системы координат Q^k, где k = 1, 2, 3 (Рис. 1).

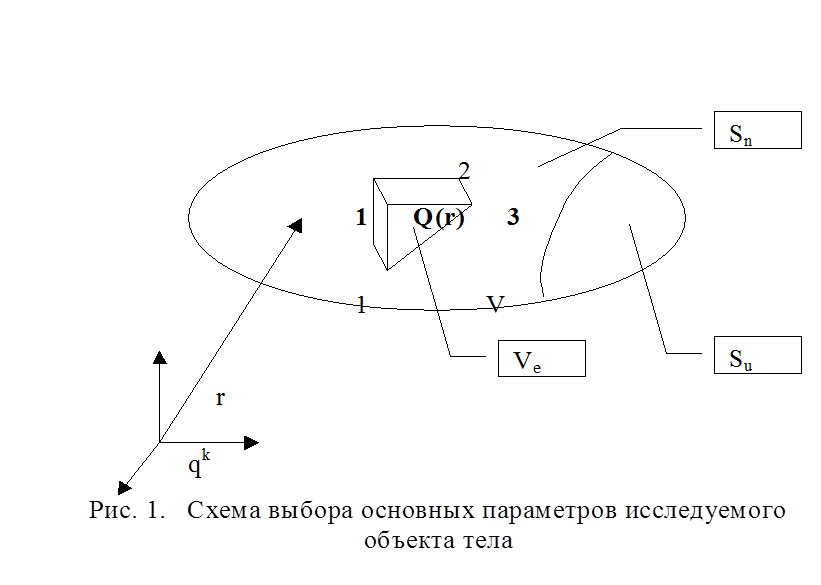При решении задачи теплопроводности Q = t – тензор ранга ноль, температура, скаляр. Искомое поле Q должно удовлетворять во внутренних точках тела объема V дифференциальному уравнению:

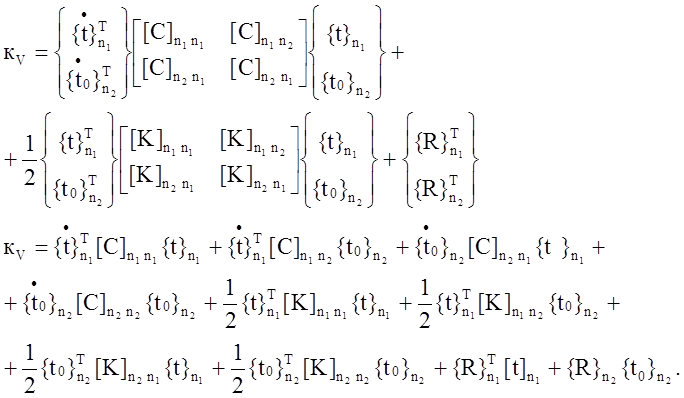
где L₂ – тензорный дифференциальный оператор второго порядка, содержащий производные по координатам до второй включительно.

На границе тела (на поверхности S = S_n+S_u) поле Q должно удовлетворять граничным условиям Неймана (на части поверхности S_u)

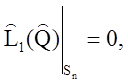
и Дирихле (на части поверхности S_u)

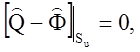
где L₁ – тензорный дифференциальный оператор первого порядка;

Ф – заданное на части поверхности S_u значение тензора Q/

Для большинства краевых задач существует эквивалентное вариационная постановка, при которой поле Q должно удовлетворять граничным условиям Дирихле и обеспечивать минимум функционала;

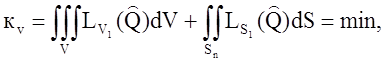
где L_v1 и L_s1 – скалярные дифференциальные операторы первого порядка.

МКЭ позволяет получить приближённое решение краевой задачи в вариационной постановке () - () при применении этого метода исследуемую область V разбивают на совокупность элементов е объёмом V_e так, что

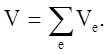
При этом

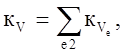
где k_Ve интеграл () вычисленный по объёму V_e.

Зависимость тензора Q от координат внутри элемента е аппроксимируют значениями Q_em этого тензора в узлах k = i, j, m, …

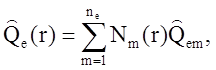
где N_m(r) – функция формы [], определяющая вид зависимости (); n_e – число узлов в элементе е.

После приближённого вычисления интегралов к_ve на основании выражения () получают функциональную зависимость интеграла () от узловых значений Q_ek тензора Q, которые определяют из условий экстремума

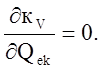
Соотношение () позволяет получить разрешающую систему уравнений относительно неизвестных узловых значений Q_m (m=1, …, n; n – общее число узлов дискретной схематизации исследуемой области). Решение такой системы позволяет на основании () найти аппроксимацию искомого тензорного поля Q(r).

Таким образом, МКЭ позволяет привести решение краевых задач к решению однотипных систем алгебраических уравнений, обеспечивает большую степень автоматизации получения системы разрешающих алгебраических уравнений при составлении программ. Одним из преимуществ является универсальность по отношению геометрии исследуемой области.