Методика численного анализа задачи определения теплового состояния на основе формирования и решения уравнения теплопроводности методом конечных элементов, страница 2

1.2  Формулировка основных соотношений при решении задачи нестационарной теплопроводности

В рассматриваемой задаче для точек области, ограниченной замкнутой поверхностью S = S_n+S_u, определению полежит зависимость температурного поля Q = t(r, t) от координат r(q^k) и времени t. Искомое поле удовлетворяет:

уравнению теплопроводности

начальному условию

условиям конвективного теплообмена на поверхности S_n

условиям Дирихле

Здесь Ñ - дифференциальный оператор Гамильтона: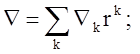

П – тепловой поток определяемый градиентом Ñt температуры t в соответствии с законом Фурье:

l - тензор констант теплопроводности, определяемый совокупностью “физических” компонент l_{<k, l>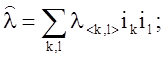}:  r₀ – плотность материала; a - коэффициент теплоотдачи; t_¥ - температура среды; q – поток теплоты через поверхность S_n в направлении внешней нормали; Ф(r, t) – температура, заданная на поверхности S_u.

Для рассматриваемой нестационарной задачи теплопроводности возможен вариационный подход, в соответствии с которым искомое поле температур t(r, t) удовлетворять граничным условиям () и минимизировать в каждый в каждый фиксированный момент времени t функционал

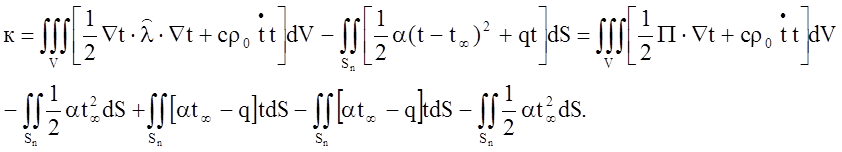
Покажем, что решение задачи нестационарной теплопроводности в вариационной постановке удовлетворяет уравнениям () – (). Условие экстремума функционала имеет вид

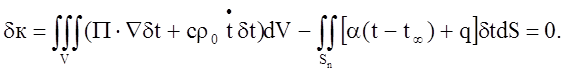
Для преобразования первого слагаемого в вариационном выражении () используем тождество

и формулу Остроградского – Гаусса

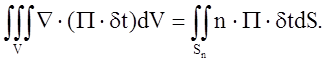
C учётом граничного условия () dt|_Sn = 0 получим

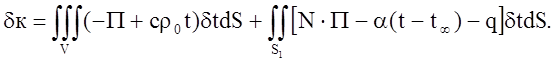
Вследствие произвольности вариации dt отсюда получаем уравнения () – () задачи нестационарной теплопроводности в прямой постановке.

1.3  Численный анализ нестационарных полей температур в элементах конструкций с помощью МКЭ

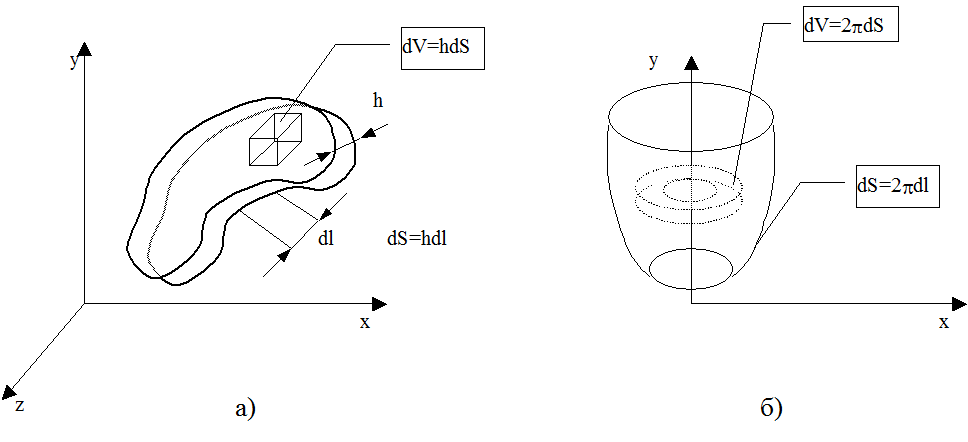
Рассмотрим методику использования МКЭ в соответствии с соотношениями () – () для решении задачи нестационарной теплопроводности в вариационной постановке () – (). Разобьем исследуемую область на совокупность элементов (рисунок 2). Аппроксимируем температурное поле t внутри элемента е в каждый фиксированный момент времени t в соответствии с выражением () узловыми значениями t_m (m = 1, …, n_e):

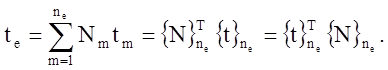
Здесь n_e – число узлов элемента е; N_m – функция формы, зависящая от координат q^k (N_m = 1 в узле m и N_m = 0 во всех остальных узлах).

Принятая аппроксимация () зависимости t_e(q^k) позволяет вычислить интеграл () по объёму V_e.

Считаем, что тензор констант теплопроводности изотропен l = lЕ, где l - коэффициент теплопроводности; Е – единичный тензор.

Рис. 2.  Схемы дискретизации типичных модельных элементов

Таким образом, первое слагаемое в подынтегральном выражении функционала () имеет вид

С учётом аппроксимации () получаем

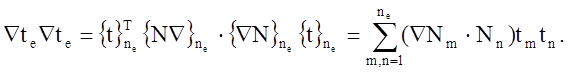
Аналогично

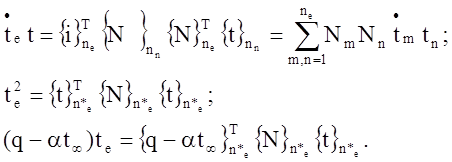
Здесь индексом n*_e помечены отличные от нуля компоненты векторов {t}, {N} и {q-at_¥}, которые соответствуют, узлам, лежащим на поверхности S_ne.

Таким образом, функционал () по объёму V_e на основании принятой аппроксимации () – () преобразуем к виду

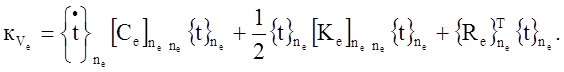
Здесь

[I₁], [I₂], [I₃]-интегралы ,определяемые размерами и формой элемента e ,а также видом формы {N}_ne:

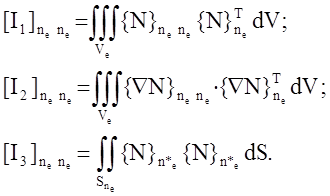
Выражение () позволяет с помощью соотношения () аппроксимировать функционал () для исследуемого объёма V в виде функции узловых температур {t}_n:

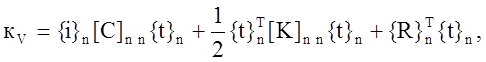
где n – общее число узлов в объёме V; [С], [К], {R} – матрицы, получаемые суммированием по элементам е матриц () – ():

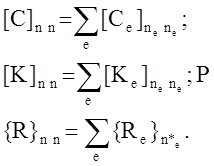
Таким образом, задача нестационарной теплопроводности сводится к отысканию в каждый фиксированный момент времени t температур {t}^T_n=({t}^T_n1; {t^T_n2}) в узлах n = n₁₊ n₂, минимизирующих функцию () в виде