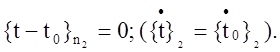
Непосредственное исключение заданных узловых значений {t}n2
системы разрешающих уравнений связано со значительными трудностями на этапе программирования.
Пронумеруем листы так, чтобы условиям () удовлетворяли последние n2 компонента вектора {t}n:
![]()
C учётом граничных условий () и обозначений () аппроксимируем функционал кV в виде
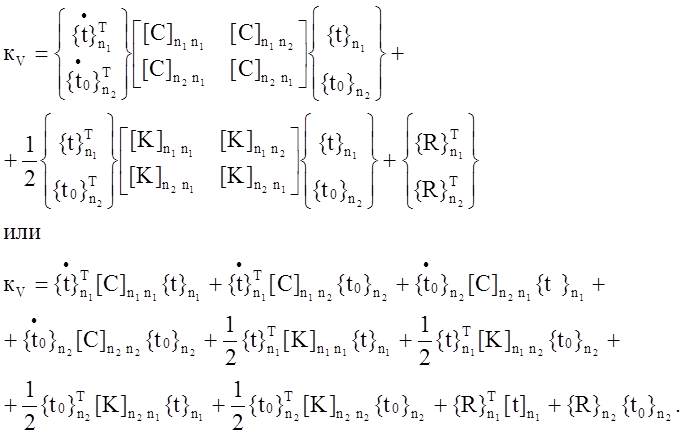
В точке экстремума
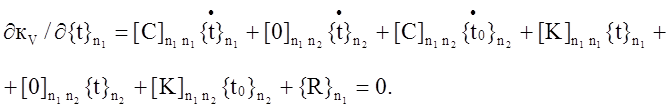
Условия () автоматически следуют из решения системы дифференциальных уравнений
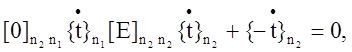
где ![]() - единичная матрица.
- единичная матрица.
Объединив уравнения () и (), получаем
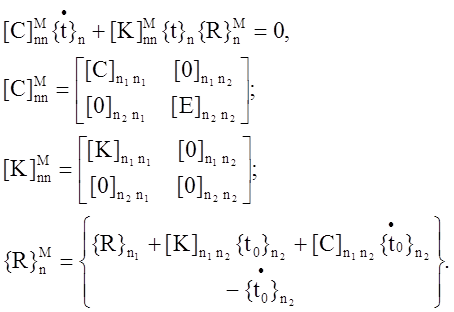
Формулы () определяют порядок модификации матриц [С]nn, [К]nn и {R}n для учёта граничных условий Дирихле (). Аналогично можно показать, что решение стационарной задачи теплопроводности сводится к системы линейных алгебраических уравнений вида
![]()
где
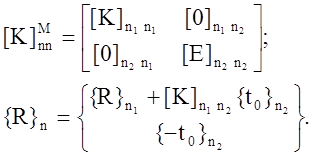
Преобразовывая () и () сохраняют параметры матриц и не нарушают симметрии.
Таким образом, МКЭ позволяет свести задачи нестационарной теплопроводности к решению системы обыкновенных дифференциальных уравнений () первого порядка относительно узловых температур и системы алгебраических уравнений ().
Рассмотренный вариант МКЭ позволяет решать задачи нестационарной теплопроводности в линейной постановке, а так же с учётом зависимости теплофизических констант от температуры и времени. В последнем случае время счёта значительно увеличивается, так как при этом необходимо вычислять матрицы [C]nn, [K]nn, {R}n на каждом шаге интегрирования по времени.
2. ПЕРЕХОД ОТ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ К РАСЧЁТНОЙ МОДЕЛИ
Тепловое состояние среды выражается уравнением
![]()
Для того чтобы решить это уравнение представим тело суммой элементарных объёмов и поверхностью
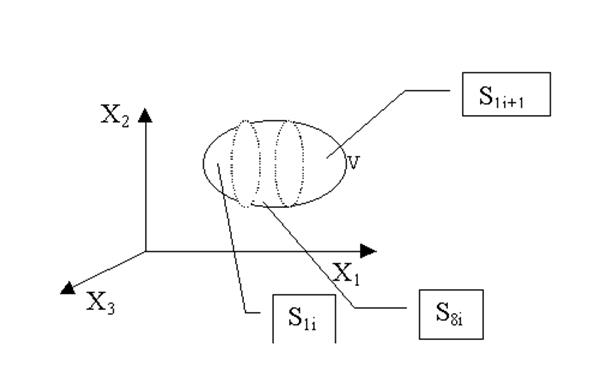
Рис. 3.
Тело объёмом V ограниченное поверхностью S при его дискретном представлении состоит из k элементов объёма
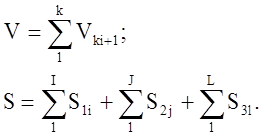
I, J, L – части на поверхности S.
Каждый элемент Vk имеет теплофизические свойства: lk (Вт/см*град.), Сrk – (Дж/см3*град.), и внутренние теплопотоки Qk (Вт/см3).
На поверхности Si происходит конвективный теплообмен с интенсивностью ai(Т - Т∞), ai (Вт/см*град.):
ai – теплопроводность стенки;
Т∞ – температура среды.
На поверхности S2 действуют теплопотоки qi (Вт/см2).
На поверхности S3 – {Т}S3
В произвольный момент времени с учётом аппроксимации тела и теплофизических параметров тепловой баланс описывается дифференциальным уравнением первого порядка
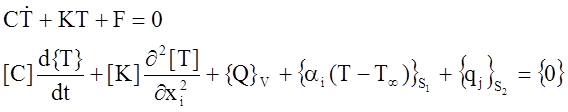
При {Tl}S2
Где [C] – матрица характеристик теплоёмкости;
[K] – матрица характеристик теплопроводности;
{Q} S2 – вектор нагрузок
{ai(Т - Т∞)}S – вектор нагрузок вызванный теплоотдачей на поверхности S1;
{qj} S2 – вектор нагрузок вызванный теплопотоками на S2;
{Тl} – вектор нагрузок вызванный температурой на S3;
n – число неизвестных.
3. ПРИМЕНЕНИЕ ИЗОПАРАМЕТРИЧЕСКОГО КВАДРАТИЧНОГО ЭЛЕМЕНТА ДЛЯ РЕШЕНИЯ ЗАДАЧ ТЕПЛООБМЕНА
Рассмотрим задачу переноса тепла за счёт конвекции и определим распределение температуры по длине стержня. Уравнение для линейного элемента имеет вид
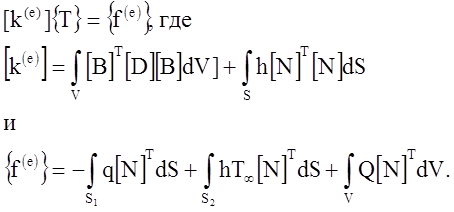
Но, так как мы используем квадратичный элемент вместо линейного элемента интегралы, приведённые выше, должны быть вычислены заново.
Во внутренних точках элемента температура определяется с помощью матрицы функции формы [N]:
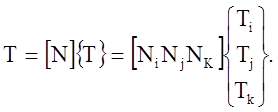
Матрица градиентов имеет вид
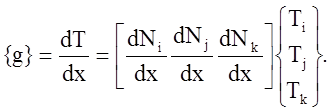
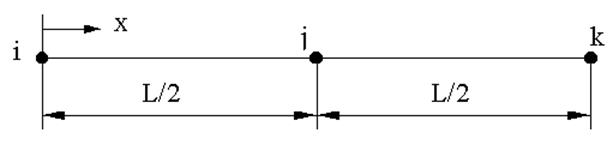
Рис. 3. Квадратичный одномерный элемент
Функция формы для квадратичного элемента имеет вид
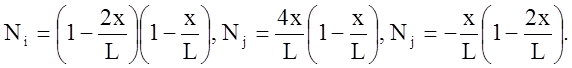
С помощью функции формы в () получаем
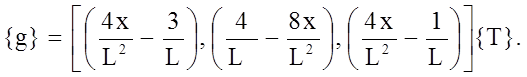
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.