Механика \ Численная технологическая механика

Методика численного анализа задачи определения теплового состояния на основе формирования и решения уравнения теплопроводности методом конечных элементов, страница 4

Учитывая, что в данном случае [D] = [Kxx] и dV = Adx, интеграл

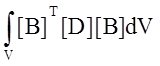
запишем в виде

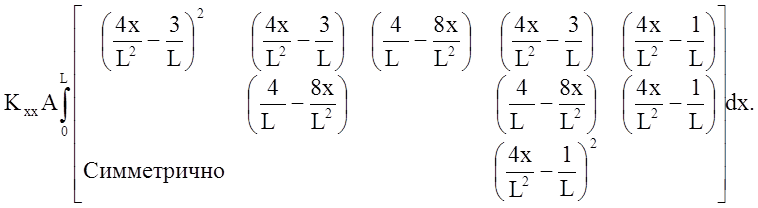
Отсюда имеем

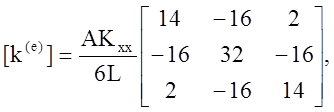
где А – площадь поперечного сечения элемента. Конвективная часть [k(e)] даётся формулой

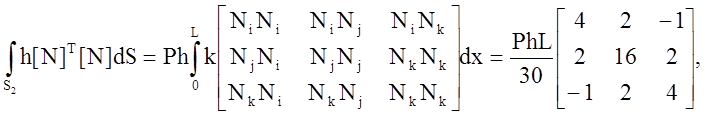
где Р – параметр элемента. Конвективная составляющая вектора столбца {f(e)} имеет вид

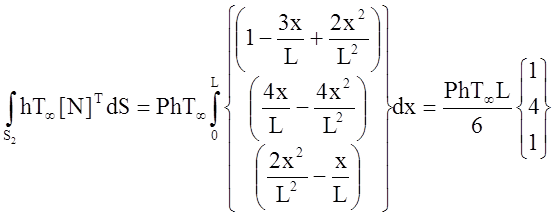
Если конвективный теплообмен наблюдается на конце элемента, например в узле i, то Ni = 1, Nj = Nk = 0 и поверхностный интеграл имеет вид

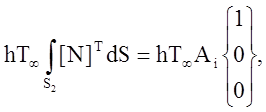
где Аi – площадь поверхности в узле i. Наличие теплообмена в узле i сказывается на матрице теплопроводности [k(e)] благодаря поверхностному интегралу

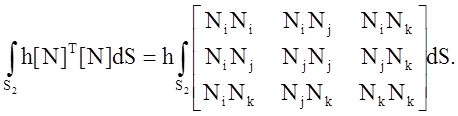
Интегрируя по поверхности, содержащей узел i, получаем

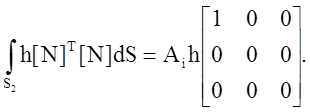
Интеграл от теплового потока q идентичен уже вычисленному интегралу (), поэтому можно сразу записать

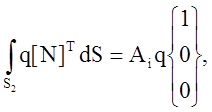
где q – заданный поток в узле i. Объёмный интеграл, включающий источник тепла Q, вычисляется так же легко:

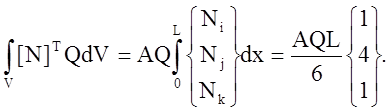
3. ЕСТЕСТВЕННАЯ СИСТЕМА КООРДИНАТ. ПРЕОБРАЗОВАНИЯ КООРДИНАТ. МАТРИЦА ЯКОБИ

Естественная система координат обладает определённым преимуществом при рассмотрении двумерных и трёхмерных элементов, так как она позволяет деформировать границы этих самых элементов. Безразмерная система координат может быть так же введена и для одномерных элементов. Однако упомянутое преимущество здесь носит главным образом академический характер. Оно упрощает иллюстрацию самого понятия локальных координат и некоторых вычислительных операций. В настоящем разделе будет рассмотрена естественная система координат для одномерного элемента.

Естественной системой координат для одномерного элемента служит относительная длина определяемая как        где x - координата. Начало отсчёта x выбрано в средней точке элемента (см. рисунок 1). Функции формы N могут быть определены с помощью формулы (), если только f выражены теперь через x вместо х.

В настоящем разделе будет проиллюстрировано вычисление матрицы элемента. Для дальнейших выкладок нам потребуются формулы преобразования координат вида

или

Функции f(x) и g(x) предполагаются взаимооднозначными.

Интерполяционное соотношение для скалярной величины, для температуры, имеет вид

где

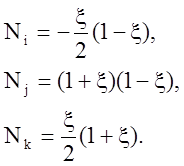
Формулу преобразования координат можно записать, используя такую же комбинацию функций формы, но только в качестве узловых параметров нужно взять координаты узлов:

где Nb - те же функции формы, что и в формуле ().

Вычисление dNb/dx теперь не представляет труда, если вспомнить, что

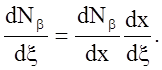
Обращая последнее равенство, имеем

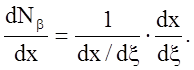
Величина dx/dx называется матрицей Якоби преобразования координат; далее она будет обозначаться через [J]. Для одномерного случая [J] есть матрица размером 1×1, которая вычисляется по формуле


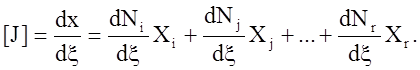
6. ЗАКЛЮЧЕНИЕ

Рассмотрена методика численного анализа задачи определения теплового состояния на основе формирования и решения уравнения теплопроводности методом конечных элементов. Методика предполагается использовать для расчета долговечности конструкций при термохимическом нагружении. Задача нахождения распределения температуры в  объёме рассчитываемой на прочность детали, в зонах локализации напряжений решается в виде пошагового решения, которой будет приведено в дальнейшем.

7. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Ши Д. Численные методы в задачах теплообмена.  -М.:  Мир, 1988г. –544с.

2. Зенкевич О. Метод конечных элементов в технике./Пер. с англ. -М.:  Мир, 1986г. –326с.

3. Гусенков А.С., Котов В.А. длительная неизотермическая усталость материалов конструкций. -М.: Машиностроение, 1984.-240 с.

Скачать файл