Модели долговечности при малоцикловом нагружении

Модели долговечности при малоцикловом нагружении

1.Малоцикловая усталость

Малоцикловая усталость – повреждение материала или детали в результате повторных упругопластических деформаций, приводящих к разрушению через ограниченное число циклов нагружения N≤10⁵. От обычной многоцикловой усталости малоцикловая усталость отличается более значительной (десятые доли процента и более) шириной петли гистерезиса в каждом цикле нагружения. Кроме этого, малоцикловое нагружение деталей авиационных двигателей, реализующееся в процессе повторения полетных циклов и изменения режимов двигателя, характеризуется значительно меньшей частотой действия нагрузок, чем при усталостных разрушениях.

Малоцикловая усталость наблюдается обычно в деталях, имеющих зоны концентрации напряжений. Например, в дисках такими зонами являются отверстия под стяжные болты и каналы для подвода охлажденного воздуха, шлицы в ступичной части, пазы замковых соединений, валы у отверстий для подвода смазки и т.п. 

Характер разрушения при малоцикловой усталости определяется величиной, действующей в цикле нагрузки; при больших нагрузках и малом числе циклов N_р(до 10²) имеют место признаки статического повреждения, наблюдается остаточная деформация; при уменьшении нагрузки и увеличении числа циклов(до 10⁴-10⁵) разрушение носит усталостный характер с выраженными следами сдвиговой деформации в виде скольжения. В промежуточной зоне можно наблюдать признаки обоих видов разрушения.

Малоцикловая усталость характеризуется величиной действующих напряжений или деформаций. Нагружение, при котором от цикла к циклу остаются неизменными величины действующих напряжений, называют «мягкими», а нагружения, при которых сохраняются постоянными величины деформаций, - «жесткими». Примером «мягкого» нанружения является действие внутреннего давления газового потока на оболочку и корпус ГТД в каждом цикле запуска – остановка двигателя. «Жесткое» нагружение наблюдается в зонах концентрации напряжений.

Степень «жесткости» нагружения той или иной зоны детали выявляется расчетом поцикловой кинетики величины напряжений и деформаций.

2. Кривые деформирования при малоцикловом нагружении

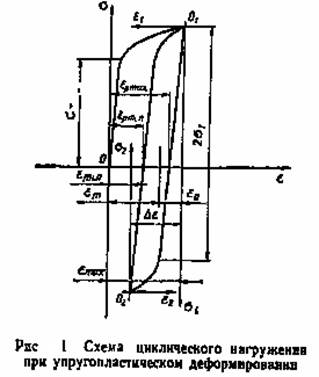
Основные характеристики цикла нагружения, относящегося к стабилизованной стадии процесса, показаны на рис.1. Цикл характеризуется амплитудой и средним значением общей и пластической деформации:

;                                           

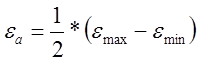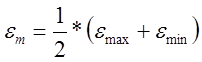 ;                       (1)                          

;

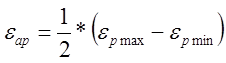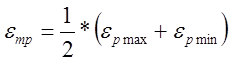.                  (2)

В расчетных уравнениях часто используется величина размаха общих или пластических деформаций:

;

.                  (3)             

С использованием величин напряжений соответствующие характеристики записываются так:

;

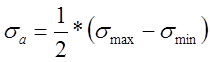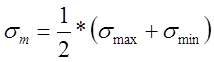;                   (4)

.                                       (5)

В расчетах можно использовать зависимость σ – ε, построенную по начальной диаграмме деформирования, характеризующей исходное нагружение. Приближенное построение полного цикла σ – ε, показанного на рис.1, осуществляется по принципу Мазинга. При этом разгрузка из точки О₁ рассматривается как процесс упругого деформирования под действием нагрузки с обратными знаками до величины σ=2σ_т аналогично деформированию при исходном нагружении. Процесс деформирования от точки О₂ до точки О₁ считается аналогичным процессу, протекающему на отрезке от точки О₁ до точки О₂.

Схема циклического деформирования по Мазингу показана на рис.2. Применение принципа Мазинга допустимо при малых величинах упругопластических деформаций. Для материалов, у которых исходная диаграмма деформирования существенно отличается от диаграммы деформирования в последующем цикле, при построении циклограмм σ – ε следует использовать не исходный, а следующий за ним цикл. Полученная таким образом циклограмма σ – ε используется в расчетах для определения величин, действующих в детали напряжений и деформаций (или их размахов) Δσ и Δε. Предпочтительнее использовать при этом экспериментальные кривые. Если процесс стабилизации после первых десятков циклов выражен недостаточно четко, то расчет можно осуществлять с помощью зависимостей σ – ε, относящихся к этапу N=0.5N_р. В этом случае, если стабилизация процесса не наблюдается (рис.3), расчет должен производиться с использованием фактических зависимостей σ – ε, относящихся к различным значениям чисел циклов. Для построения циклограмм σ – ε и для расчета напряженно-деформированного состояния необходимо аналитическое описание исходных кривых деформирования.

При кусочно-линейной аппроксимации кривая деформирования выражается зависимостями:

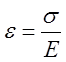     при σ≤σ_т;

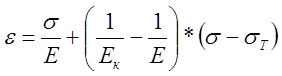    при σ>σ_т,                (6)

где Е – модуль упругости;

       σ_т – предел текучести;

       Е_к – касательный модуль.

Аппроксимация нелинейного участка диаграммы деформирования степенной функцией возможна в следующем виде:

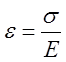     при σ≤σ_т;

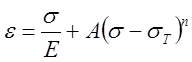    при σ>σ_т,                                     (7)

где А и n – параметры, зависящие от типа материала.

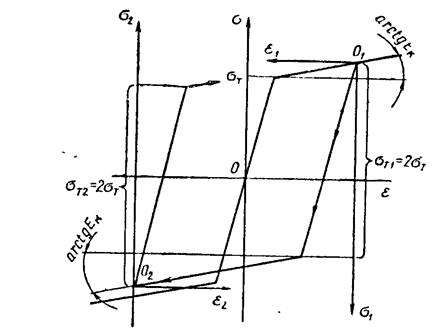
Рис.2. Схема циклического нагружения по Мазингу.

3. Кривые циклического деформирования.

Для учета деформационной анизотропии упругих постоянных, циклического эффекта Баушингера, а также изменения нелинейного участка деформирования в процессе нагружения возможно более общее преобразование кривой циклического деформирования:

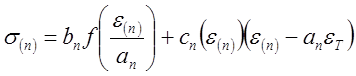 ,                      (8)

где