- число циклов до достижения заданного размера трещины;
- начальный размер трещины или дефекта, позволяющего при заданном уровне номинальных напряжений обеспечить требуемую циклическую долговечность;
- уровень номинальных напряжений, допустимый для детали, имеющей дефект заданного размера.
Для определения числа циклов, в течение которых трещина развивается от размера а= а0 до критического, когда а = ас, выражение (17) подставляется в уравнение (20). Получаемое при этом уравнение
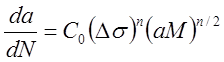 (21)
(21)
интегрируется от a=aQ до а=ас, в результате чего получают выражение для искомого числа циклов
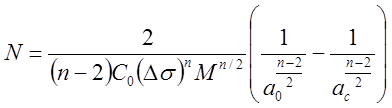 . (22)
. (22)
Приведенная формула справедлива при n≠2. Если n=2, число циклов нагружения, в течение которых происходит развитие трещин, определяется как
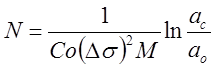 .
(23)
.
(23)
Значение функции М в (23) рассчитывается в зависимости от формы поверхности трещины, типичной для натурных деталей (см. табл. 1). Так, наиболее распространенной для дисков является уголковая трещина с поверхностью в форме четверти круга или эллипса, берущая начало от эксцентричного отверстия. Трещины, начинающиеся от внутренних дефектов (например, неметаллических округлых включений в гранульных материалах, пор в линейных сплавах) имеют, как правило, форму круга.
Критический размер трещины ас, по достижении которого происходит мгновенное разрушение, может быть определен с помощью формул, представленных в табл.1. При этом значение ΔК принимаются равными К1с – вязкости разрушения.
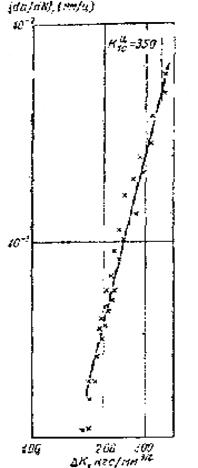 Рис. 10. Кривая развития
трещины сплава ЭВ689.
Рис. 10. Кривая развития
трещины сплава ЭВ689.
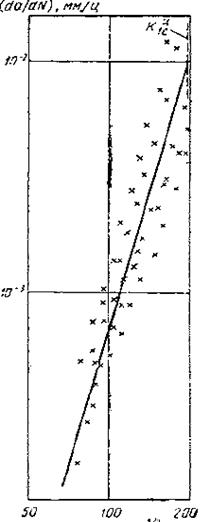 Рис 9. Кривая развития
трещины при циклическом нагружении сплава ВТ3-1.
Рис 9. Кривая развития
трещины при циклическом нагружении сплава ВТ3-1.
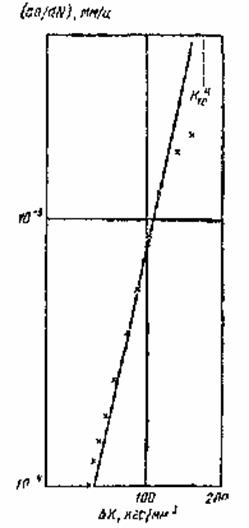
Рис.11. Кинетическая кривая развития трещины при малоцикловом нагружении гранульного никелевого сплава для дисков.
Пример расчета циклической долговечности с учетом стадии роста трещины.
Последовательность и методические особенности расчета циклической долговечности с учетом стадии развития трещины можно показать на примере диска компрессора из сплава ВТЗ-1 (рис. 12). Предполагается, что разрушение диска начинается от выкружки паза под действием окружных напряжений σθ и развивается в радиальном направлении. Как показывает анализ разрушения такого типа, трещина в диске, образующаяся при указанных далее условиях нагружения, развивается от угла паза и имеет форму четверти эллипса с полуосями а = 0,5 мм, с=1 мм.
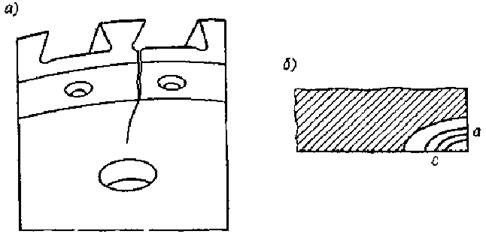
Рис.12. Трещина в диске компрессора и принятая схема развития.
При расчете приняты следующие исходные данные: материал диска — титановый сплав ВТЗ-1; ов =500 МПа; упругий коэффициент концентрации напряжений в выкружке диска ασ =2,7; Т= 20°С.
Размах коэффициента интенсивности напряжений вычисляется по формулам, приведенным в табл. 1:
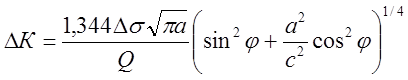 , (24)
, (24)
где Δσ=σθ.
Диаграмма деформирования сплава ВТЗ-1 представлена на рис. 13, кривая развития трещины — на рис. 9.
Определим число циклов до образования трещины. В месте образования трещины упругие напряжения с учетом их концентрации составляют
σупр=500*2,7=1350 МПа.
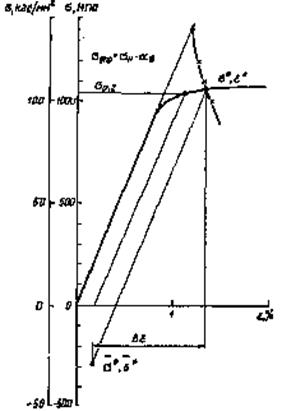
По диаграмме деформирования (см. рис. 13), используя модифицированную формулу Нейбера в виде
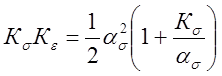 или
или
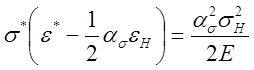 ,
,
находим напряжение и деформацию в упругопластической области: σ*=1060 МПа, ε* = 0,0134. После разгрузки напряжения в точке поверхности надреза σ¯*= —290 МПа, ε¯* = 0,0017. Размах деформации в первом цикле составляет
Δε = ε*-ε¯*= 0,0134—0,0017=0,0117.
Рис.13. Диаграмма деформирования сплава ВТ3-1 при Т=20°С и распределения напряжений и деформаций в точках паза.
Амплитуда напряжения цикла определяется следующим образом:
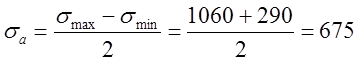 МПа.
МПа.
Среднее напряжение цикла находится из выражения
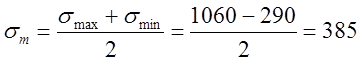 МПа.
МПа.
Амплитуда напряжения эквивалентного симметричного цикла составляет
![]() МПа.
МПа.
Число циклов до образования трещин Nо.тр находим по экспериментальной кривой малоцикловой усталости при симметричном цикле для гладких образцов : lgN=7,495-0,0513σа. Для σа симэкв=867,5 МПа (86,75 кгс/мм2) Nо.тр=1110 ц.
В случае отсутствия экспериментальных данных для титановых сплавов при Т=20 С° может быть использована зависимость Мэнсона, включающая только упругую составляющую суммарной деформации
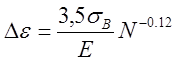 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.