где Δε – размах деформации, рассчитанный по эквивалентной амплитуде напряжений симметричного цикла (Δε=0,0151). Расчетное число циклов до образования трещины Nо.тр составляет около 910 циклов. По экспериментальным данным 1110 ц.
На стадии развития трещины число циклов, в течении которых трещина разрастается от начального размера аi до критического ас, рассчитывается по формуле (22), где за начальный размер трещины принимается 0,5мм. Критический размер трещины определяется из условия равенства ΔК критическому значению К1с, рассчитанному по формуле (24). При значениях К1с=195 кгс/мм3/2 и принятом постоянном отношении полуосей эллипса а/с=ас/с=0,5, получаем
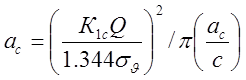=7,6
мм.
Тогда в соответствии с формулой (22) число циклов, в течение которых трещина развивается до критической величины, составит Nр.тр=11700 ц. Суммарная циклическая долговечность NΣ=Nо.тр+Nр.тр=1110+11700=12810 ц.
Принимая запас по циклической прочности равным 5, получим допустимую циклическую долговечность Nэ=2560 ц.
Замковые соединения типа «ласточкин хвост».
В качестве рассмотрено
распределение напряжений в соединении типа «ласточкин хвост»
лопаток и дисков компрессора Изучалось
распределение напряжений в наиболее напряженной области соединений – пазах
дисков, ибо именно здесь возникают типичные разрушения. Выбраны типичные
значения углов раствора замков (α=45,60,70°), характерные для отечественных и
зарубежных конструкций.
В расчетах принимали, что рабочие грани пазов диска, выполненного из стали ЭИ-961, нагружены давлением то лопатки, распределенным по треугольному закону. Близкий к таковому закону распределения давлений получен экспериментально методом фотоупругости. Кривая деформирования материала также получена экспериментальным путем. Взаимовлиянием лопаток пренебрегли, пологая, что угол развала (между осями) лопаток достаточно велик.
Результаты расчетов приведены на рис. 14-16. Из рисунков ясно, что наибольшие напряжения возникают в пазе диска, примерно посредине галтели. Если ввести в рассмотрение условный коэффициент концентрации напряжений Кσ=σ0max/σ0, равный отношению максимального контурного напряжения во впадине к номинальному растягивающему, то оказывается, что в замке с углом раствора 70° Кσ=2,84, а в замке с α=45° Кσ=3,00. Отсюда видно преимущество замков с большим углом α. Отметим, что с ростом α наиболее напряженная точка смещается к рабочей грани замка. Характер распределения напряжений не меняется, а изменяются лишь форма и размеры зоны нелинейных деформаций (заштрихованы на рис. 14-16).
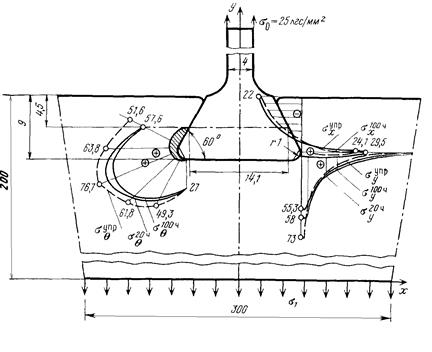Рис.
14
Рис.15.
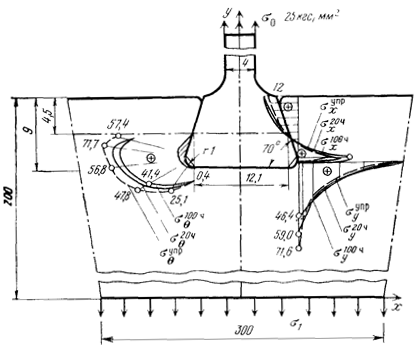
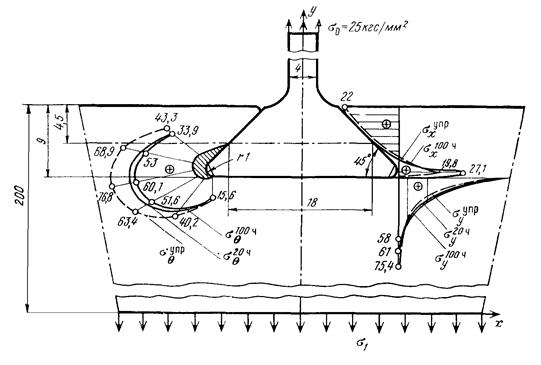
Рис.16.
Увеличение радиуса скругления впадины диска снижает концентрацию напряжений, однако возможности увеличения радиуса, как и угла раствора, ограничены нарастанием контактных давлений в соединении. При большем угле раствора, кроме того, уменьшается размер перемычки между пазами, и меньшее число лопаток может быть размещено на ободе диска.
Кинетика напряженного и деформированного состояния при нагружении замков за пределами упругости имеет много общего с другими деталями: максимум напряжений σу смещается в тело диска и находится вблизи грани упругой и нелинейной зон; теоретический коэффициент концентрации напряжений существенно снижен.
На рис. 17 приведены результаты экспериментального исследования распределений напряжений в замке «ласточкин хвост» с углом α=70° методом фотоупругости. Напряжения даны в безразмерных величинах. Для получения натуральных напряжений в модели эти величины нужно умножить на оптическую постоянную материала σ0(l)=32,5 кгс/см2 полос. Экспериментальное значение коэффициента концентрации напряжений (в упругости) равно Кσ=3,20, что достаточно близко к приведенному расчетному. Характер распределения напряжений полностью соответствует расчетным данным.
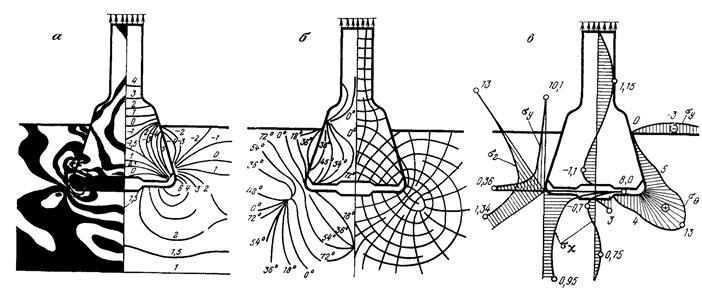
Рис.17. Результаты расшифровки экспериментальных данных:
а- картина полос и изонахик; б – изоклины и изостаны; в – эпюры напряжений.
В заключении отметим, что в экспериментах замечено существенное влияние на величину коэффициента концентрации напряжений трения на контактной поверхности лопаток и диска. Полученное опытное значение Кσ=3,25 соответствовало контакту смазанных поверхностей. Расчет же проводился без учета трения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.