Модели долговечности при малоцикловом нагружении, страница 4

В этом случае размах коэффициента интенсивности напряжений возрастает за счет роста длины трещины по мере увеличения чис­ла циклов.

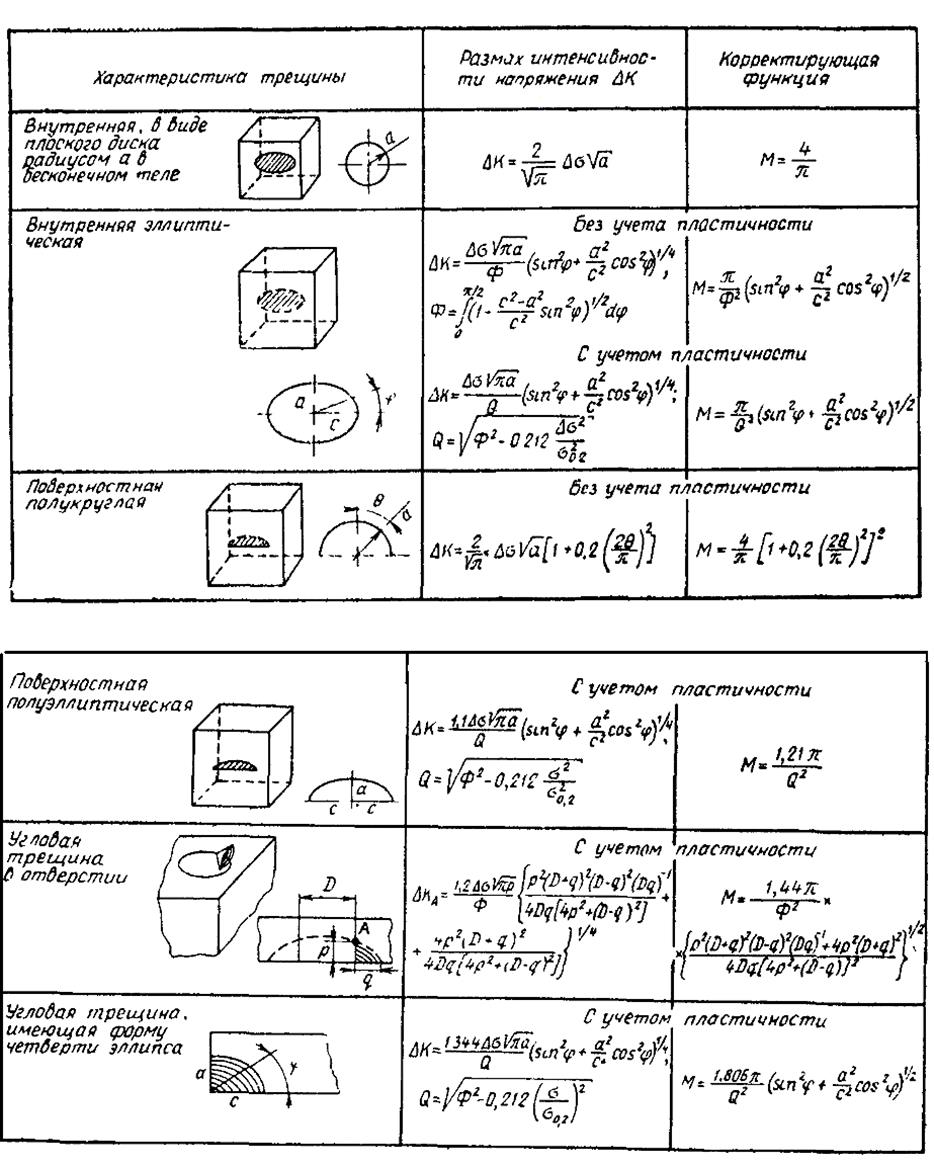
Некоторые варианты формул, используемых для определения ΔК и М в зависимости от формы поверхности трещины и ее рас­положения в детали, приводятся в табл. 1. Пользуясь этими фор­мулами и зная значение размаха напряжений Δσ, действующего в детали, а также форму трещины, можно определить критические размеры трещины, при которых начинается ее самопроизвольный лавинный рост, т. е. разрушение детали.

Состояние разрушения соответствует условию

Δ К = К_1с,                                         (18)

где К_1с—вязкость разрушения или предельное значение коэффи­циента интенсивности напряжений, соответствующие такому соче­танию Δσ и а, при котором начинается лавинный рост трещины.

Вязкость разрушения К_1с определяют на стандартных образ­цах, имеющих соотношение размеров (ширины и толщины), при котором реализуется плоское деформированное состояние в зоне распространения трещины; К_1с может быть определено как при однократном статическом, так и при циклическом нагружении.

 Таблица 1.

Величины К_1с, полученные при циклическом нагружении, несколь­ко ниже величин, определяемых при статическом нагружении. Зна­чения К_1с для ряда дисковых сплавов, определенные как предель­ные величины ΔК при циклических испытаниях плоских образцов, нагружаемых по схеме трехточечного изгиба (пульсирующий цикл при комнатной температуре), представлены в табл. 2.

Величины К_1с при повышенных температурах определены пересчетом как

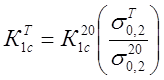                       (19)

Таблица 2.

С п л а в	Т,°С	К1с- кгс/мм3/2(МПа*м1/2)
ВТЗ-1	20	195(60)
	400	118(36)
ВТ-8	20	220 (64)
	400	150(46)
ВТ-9	20	210(65)
	400	134(41)
ЭИ698ВД	20	350(108)
	650	280 (87)
Опытный дисковый сплав, σв ≥ 1300 МПа	20 650	260 (80) 250 (77)
Опытный высокопроч­ный дисковый сплав, σ≥1500 МПа	20 650	150(46) 135(42)

6.2. Развитие трещины при циклическом нагружении.

В качестве модели развития трещины при циклическом нагру­жении, используемой как исходная информация при оценке сопро­тивления разрушению деталей с трещиной, принимается зависи­мость скорости роста трещины da/dN от размаха коэффициента интенсивности напряжений ΔК. Эта зависимость, как это следует из рис. 9,10 и 11, для титанового сплава ВТЗ-1, а также дисковых никелевых сплавов (ЭИ698ВД и опытного с σ_в ≥1300 МПа, полученного методом гранульной металлургии) удо­влетворительно описывается степенным уравнением вида:

                                                    da/dN=C_о(ΔК)ⁿ.                                     (20)

Постоянные Со и п для некоторых дисковых титановых и ни­келевых сплавов при Т = 20°С представлены в табл.3 (рассчита­ны в размерностях: ΔК — в кгс/мм^3/2, da/dN в мм/ц). В табли­це приводятся значения ΔК, в пределах которых справедливо урав­нение (20). При значениях ΔК выше указанных трещина разви­вается самопроизвольно; нижние значения представленных об­ластей принимаются за пороговые, при которых трещина не растет.

Таблица 3.

Сплав	Постоянные в уравнении.
	n	С0	Пределы   применимости ΔК, кгс/мм3/2(МПа-м1/2)
ВТЗ-1	3,97	7, 87*10-12	70- 190(22 — 60)
ВТ-8	3,17	1,38*10-10	80 — 220 (25 - 69)
ВТ-9	2,91	6,06*10-10	60 — 200(19-63)
ЭИ698В9	4,34	4,47*10-14	160 — 320(50— 100)
Опытный дисковый сплав, σв≥1300 МПа	4,48	8,31*10-13	80 — 260 (25 — 82)
Высокопрочный диско­вый сплав, σв≥1500 МПа.	7,15	1*10-17	70-120(22 — 38)

Уравнения, соответствующие кривым, представленным на рис. 9—11, рассчитаны методом минимальных средних квадратических отклонений по результатам испытаний 2—10 образцов, циклически нагруженных изгибом. Уравнение (20) позволяет оценить работоспособность конструкции из этих сплавов при на­личии трещины, т. е. определить: