Условия эквивалентности разных напряженных состояний выражаются через интенсивность размахов пластической и полной деформации.
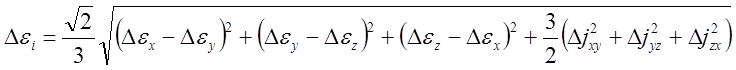 (11).
(11).
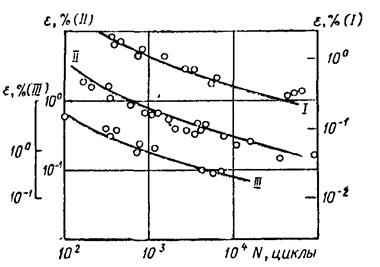
На рис.7 даны подтверждающие эту зависимость кривые малоцикловой усталости, построенные на основании расчета в приведенных деформациях для случаев испытаний образцов на изгиб, кручение и растяжение-сжатие. Доказательством справедливости этого вывода являются также результаты статистического анализа испытаний при изотермическом и неизотермическом нагружении в неодинаковых условиях, как по режимам термомеханического нагружения, так и по видам сложного напряженного состояния.
Для определения долговечности в условиях «жесткого» малоциклового нагружения и сложного напряженного состояния используют условие разрушения Мэнсона, полученное для случая одномерного напряженного состояния, где величина размаха полной деформации заменяется размахом эквивалентной деформации, определенным из уравнения (11).
При проведении проверочных расчетов, когда по внешней нагрузке определяются коэффициенты запасов прочности, оценку работоспособности материала или детали целесообразно вести по допускаемым напряжениям.
Предельные состояния материла при различных соотношениях могут быть описаны выражением:
![]() (12)
(12)
где
σi – интенсивность напряжений;
σ1, σ2, σ3 – главные напряжения;
λ0,… λ3 – параметры материала, определяемые через пределы прочности на растяжение, сжатие, кручение и внутреннее давление.
В частном случае можно принять условие эквивалентности в соответствии с критерием Мора:
σэкв=σ1- χσ3 (13)
или по критерию Писаренко-Лебедева:
σэкв=χσi+(1-χ)σ1. (14)
В равенствах (13), (14)
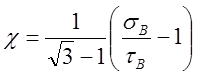 .
(15)
.
(15)
Экспериментальное подтверждение пригодности зависимости (14) для трех типов, наиболее часто используемых в деталях авиационных двигателей, материалов показано на рис.8. Испытания на малоцикловую усталость проводились в диапазоне 0≤σ1/σ2 <∞ при симметричном цикле нагружения.
С целью учета влияния величин средних значений деформаций и напряжений, действующих при асимметричных циклах нагружения, в соответствующих расчетных зависимостях для одномерного состояния в качестве эквивалентных указанным величинам следует использовать наибольшее среднее значение главных деформаций и напряжений.
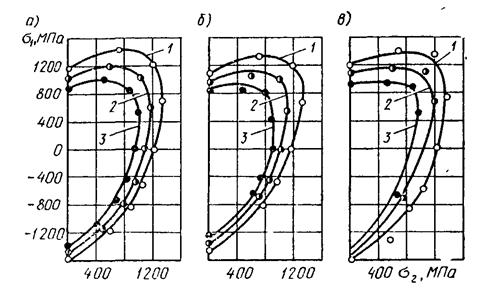
Рис.8. Результаты испытаний на малоцикловую усталость при сложном напряженном состоянии и мягком режиме нагружения легированной стали ЭИ961, титанового сплава ВТ-8 и никелевого сплава ЭИ698.
6. Расчет циклической долговечности с учетом периода развития трещины.
6.1. Основные положения и термины механики разрушения
Исследования малоцикловом усталости, рассмотренные выше, позволили установить связь между циклически действующим напряжением пли деформацией (Δσ или Δε ) и долговечностью Np, в которую входят две составляющие — числа циклов до образования макротрещины глубиной 0,5—1,0 мм — Nо,тр и числа циклов, в течение которых трещина развивается до полного разрушения Nо,тр. Изучение второго этапа разрушения, определяемого закономерностями развития трещины, составляет одну из задач механики разрушения — современной отрасли знания, основой которой явились модели хрупкого разрушения Гриффитса, Ороваш, Ирвина. Согласно этим моделям, развитие трещины связано с высвобождением запасенной в теле упругой энергии. Условие, при котором освобожденная упругая энергия превышает величину энергии, затрачиваемой на образование свободной поверхности трещины, соответствует критическому состоянию, т. е. началу самопроизвольного развития трещины.
В качестве характеристики сопротивления материала развитию трещины в механике разрушения используются значения коэффициентов интенсивности напряжении К, являющихся функцией размеров трещины а и приложенного номинального напряжения σ.
В общем случае К определяется как
![]() (16)
(16)
где М — функция, зависящая от формы трещины и расположения ее относительно поверхности.
Для условий циклического нагружения с постоянным размахом напряжений Δσ формула (16) принимает вид
![]() (17)
(17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.