Филиал Федерального Государственного Образовательного
Учреждения Высшего Профессионального Образования
«Сибирский Федеральный Университет»
в г. Железногорске
Кафедра математики и естественнонаучных дисциплин
ТИПОВОЙ РАСЧЕТ
Раздел «Кратные интегралы»
(вариант № 15)
Выполнил: студентка
ФИТ 236 Ж.
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
Вопрос 1. Определение двойного и тройного интегралов. Их геометрический и физический смысл.
Определение: Двойным интегралом от функции f(x,y) по области S называется предел её интегральной суммы при λ→0:
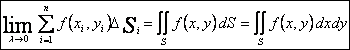 ,
,
где S – область интегрирования, f(x,y) – подынтегральная функция.
Предел интегральных сумм существует, если функция f(x,y) непрерывна в замкнутой области S.
Геометрический смысл двойного интеграла: ![]() , т.е. двойной
интеграл от функции f(x,y)≥0 на
области S равен объёму цилиндрического тела с основанием S и ограниченного сверху поверхностью z=f(x,y).
, т.е. двойной
интеграл от функции f(x,y)≥0 на
области S равен объёму цилиндрического тела с основанием S и ограниченного сверху поверхностью z=f(x,y).
Физический смысл двойного интеграла:
![]() -
масса плоской фигуры. Если масса распределена равномерно по всей фигуре, μ=const, то эта формула примет вид:
-
масса плоской фигуры. Если масса распределена равномерно по всей фигуре, μ=const, то эта формула примет вид: ![]() , где S – площадь фигуры D.
, где S – площадь фигуры D.
Определение: Если при λ→0 интегральные суммы σ имеют
предел, не зависящий ни от способа разбиения области Ω на
частичные подобласти Ωi,
ни от выбора точек Pi€ Ωi,
то этот предел называется тройным интегралом от функции f(x,y,z) по
области Ω и обозначается символом ![]() или
или
![]() . При этом функция f(x,y,z) называется
интегрируемой в области Ω.
. При этом функция f(x,y,z) называется
интегрируемой в области Ω.
Таким образом, по определению имеем: ![]()
Геометрический и физический смыслы тройного интеграла: Возвращаясь к задаче о вычислении массы тела,
замечаем, что предел ![]() есть тройной интеграл от
функции μ(P) по
области Ω. Значит,
есть тройной интеграл от
функции μ(P) по
области Ω. Значит, ![]() , где dxdydz–
элемент объема dv в
декартовых координатах.
, где dxdydz–
элемент объема dv в
декартовых координатах.
Вопрос 2. Основные свойства двойных и тройных интегралов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.